Datalore
Collaborative data science platform for teams
Backtesting a Trading Strategy in Python With Datalore and AI Assistant
This is a guest blog post by Ryan O’Connell, CFA, FRM.
Over lunch the other day, a friend mentioned his brother, a professional asset manager, swears by a simple mean reversion trading strategy. His strategy consists of buying the 10 biggest losers in the stock market each day and selling them at the close of the following trading session. I asked him if he knew which index or exchange his brother used to pick his losers from, and he told me that he wasn’t certain. As a curious casual investor, I decided to put this strategy to the test using historical data and backtest the trading strategy with Python.
Disclaimer: This article is for informational and educational purposes only and is not intended to serve as personal financial advice.

What you will learn from this backtesting tutorial
In this article, I’ll walk through the process of backtesting a daily Dow Jones mean reversion strategy using Python in Datalore notebooks. To make it accessible even for those with limited coding experience, I’ll leverage Datalore’s AI Assistant capabilities. I’ll also show how intuitive prompts can be used to create the key components of the backtest, and demonstrate Datalore’s interactive charting and reporting features to effectively analyze and share the backtest results.
To make things more challenging for myself (and easier for you), I won’t write a single line of code myself. Every line of code in this tutorial will be generated by AI as shown below:
Still, building a comprehensive backtesting system does require significant Python expertise. But for those who don’t yet possess strong Python skills, this is where Datalore’s AI code assistance comes in. With Datalore you can:
- Generate the needed code from natural language prompts, putting backtesting in reach for Python beginners.
- Leverage a cloud-hosted Jupyter environment, eliminating the need to manage your own setup.
- Create interactive, self-documenting reports to share methodology and results with stakeholders.
If you have experience with Python, you can access the example notebook of the implemented backtesting strategy here.
Understanding the basics of backtesting
Before diving into the specific strategy we’re exploring in this article, let’s take a moment to understand what backtesting is and why it’s a critical tool for any trader or investor looking to validate their trading strategies using historical data.
Backtesting is a process by which traders simulate a trading strategy on past data to see how it would have performed. This method allows traders to evaluate and refine their strategies before applying them in real market conditions. By backtesting a strategy, one can get insights into its potential profitability, risk, and other performance metrics, without risking actual capital.
The concept is based on the assumption that historical market behavior can provide insights into future market movements. While not foolproof, backtesting offers a way to statistically analyze the likelihood of a strategy’s success based on past performance.
The mean reversion strategy: a case study in backtesting
The specific trading strategy we will backtest in this article is based on the principle of mean reversion. This financial theory suggests that asset prices and returns eventually revert back to their long-term mean or average level. Our strategy involves:
- Identifying the 10 biggest losers: At the close of each trading day, we identify the 10 stocks within the Dow Jones Industrial Average (DJIA) that have declined the most in percentage terms from the previous day.
- Executing trades: We then purchase an equal dollar value of each of these 10 stocks and hold them until the close of the following trading day, at which point we sell all positions. Immediately afterward, we repeat the process by purchasing the 10 biggest losers of that day.
- Performance evaluation: To assess the viability of this strategy, we compare its performance to that of the DJIA itself, providing an “apples-to-apples” comparison to see if our mean reversion strategy would have outperformed the broader stock market over time.
The DJIA, a stock market index that tracks 30 large, publicly-owned companies trading on the New York Stock Exchange and the Nasdaq, serves as our testing ground. By applying our strategy to the constituents of the DJIA, we aim to explore the potential of mean reversion in a real-world scenario.
To objectively evaluate this strategy, we’ll use 10 years of daily price data for all current DJIA constituents. Given the complexity of accurately modeling changes in the index’s composition over time, we’ll assume that the DJIA’s constituents have remained unchanged over the past 10 years. In our evaluation, we’ll calculate common performance metrics, including:
- Annualized return
- Annualized volatility
- Sharpe ratio
- Maximum drawdown
In the sections that follow, we’ll dive deeper into the process of implementing this strategy, from retrieving historical price data to calculating performance metrics, all with the help of Python and the Datalore AI assistant.
Retrieving historical Dow Jones stock prices
Here’s a concise prompt you could provide to the Datalore AI to retrieve the constituents of the DJIA and their historical returns:
| Prompt |
| Write code to perform the following: Fetch the current Dow Jones Industrial Average constituents from Wikipedia and save them to a CSV file. Fetch 10 years of daily adjusted close prices for each constituent using yfinance and save the data to a separate CSV file. Handle any errors and print the stock symbol that caused the error. Load the constituent symbols and price data from the CSV files into a DataFrame, and handle missing data using forward fill. |
The following code was produced by the AI using this prompt to effectively complete the task:
import pandas as pd
import yfinance as yf
from datetime import datetime, timedelta
# Fetch Dow Jones Industrial Average constituents from Wikipedia
url = "https://en.wikipedia.org/wiki/Dow_Jones_Industrial_Average#Components"
tables = pd.read_html(url)
dow_jones_constituents = tables[1]
dow_jones_constituents.to_csv('dow_jones_constituents.csv', index=False)
# Fetch 10 years of daily adjusted close prices for each constituent
start_date = (datetime.now() - timedelta(days=10*365)).strftime('%Y-%m-%d')
dataframes = []
for symbol in dow_jones_constituents['Symbol']:
try:
data = yf.download(symbol, start=start_date)
data = data[['Adj Close']]
data.columns = [symbol]
dataframes.append(data)
except Exception as e:
print(f"Failed to fetch data for {symbol}")
dow_jones_data = pd.concat(dataframes, axis=1)
dow_jones_data.to_csv('dow_jones_data.csv')
# Load the data from the CSV files into a DataFrame and handle missing data
constituents = pd.read_csv('dow_jones_constituents.csv')
data = pd.read_csv('dow_jones_data.csv', index_col=0)
data_filled = data.ffill()
constituents.head()
data_filled.head()
Implementing the mean reversion strategy
Now that we have the historical price data for the DJIA constituents, we can proceed with implementing the mean reversion strategy. The steps involved are as follows:
- Calculate the daily returns for each stock.
- Identify the 10 stocks with the lowest returns (biggest losers) for each trading day.
- Simulate buying an equal amount of each of these 10 stocks at the close of the trading day.
- Simulate selling all 10 positions at the close of the following trading day.
- Repeat this process for the entire 10-year period.
Step 1: Calculate daily returns
To begin implementing the mean reversion strategy, we first need to calculate the daily returns for each stock in our data_filled DataFrame.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to calculate the daily returns for each stock in the data_filled DataFrame. |
The AI generates the following code:
daily_returns = data_filled.pct_change() daily_returns.head()
Step 2: Identify biggest losers
Next, we will identify the 10 stocks with the lowest returns (biggest losers) for each trading day.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to identify the 10 stocks with the lowest returns for each trading day in the DataFrame containing daily returns. |
The AI generates the following code:
biggest_losers = daily_returns.apply(lambda day: day.nsmallest(10).index, axis=1) biggest_losers.head()
Step 3: Simulate trades
Now, we will simulate buying an equal amount of each of the 10 biggest losers at the close of each trading day and selling all positions at the close of the following trading day. We’ll assume an initial capital of $100,000.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to simulate buying an equal amount of each of the 10 biggest losers at the close of each trading day and selling all positions at the close of the following trading day. Assume an initial capital of $100,000. |
The AI generates the following code:
# Initialize capital
capital = 100000
# Create a new dataframe to hold our capital at the end of each day
capital_over_time = pd.DataFrame(index=daily_returns.index)
# Loop over each trading day
for i in range(len(daily_returns.index) - 1):
# Select the biggest losers for the current day
losers = biggest_losers.iloc[i]
# Get the closing prices for these stocks on the current and next trading days
prices_today = data_filled.loc[daily_returns.index[i], losers]
prices_tomorrow = data_filled.loc[daily_returns.index[i+1], losers]
# Distribute our capital equally among these stocks and buy shares
shares = (capital / 10) / prices_today
# The next day, sell all shares at the closing price and update our capital
capital = (shares * prices_tomorrow).sum()
# Store our capital
capital_over_time.loc[daily_returns.index[i+1], 'Capital'] = capital
capital_over_time.head()
Step 4: Calculate performance metrics
Finally, we will calculate the strategy’s annualized return, annualized volatility, Sharpe ratio (assuming a risk-free rate of 0), and maximum drawdown.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to calculate the following performance metrics for the simulated trades: Annualized return, Annualized volatility, Sharpe ratio (assuming a risk-free rate of 0), and Maximum drawdown. Then print the calculated metrics. |
The AI generates the following code:
import numpy as np
# Calculate the return of our strategy
returns = capital_over_time['Capital'].pct_change().dropna()
# Calculate annualized return
annualized_return = (1 + returns.mean())**252 - 1
# Calculate annualized volatility
annualized_vol = returns.std() * np.sqrt(252)
# Calculate Sharpe ratio (assuming a risk-free rate of 0)
sharpe_ratio = annualized_return / annualized_vol
# Calculate max drawdown
rolling_max = capital_over_time['Capital'].cummax()
daily_drawdown = capital_over_time['Capital'] / rolling_max - 1.0
max_drawdown = daily_drawdown.cummin()
# Print out the calculated metrics
print('Annualized Return:', annualized_return)
print('Annualized Volatility:', annualized_vol)
print('Sharpe Ratio:', sharpe_ratio)
print('Max Drawdown:', max_drawdown.min())
Step 5: Compare with the Dow Jones index
To determine if our mean reversion strategy outperformed the market, we’ll compare its Sharpe ratio with that of the DJIA. We’ll use the SPDR Dow Jones Industrial Average ETF Trust (DIA) as a proxy for the Dow Jones. The point here is to find out if betting on the losers of the Dow Jones, rather than the Dow Jones itself, is a more profitable strategy in hindsight.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to: 1. Fetch the daily adjusted close prices for the DIA ETF from Yahoo Finance for the same period as the Dow Jones data. 2. Calculate the daily returns for DIA. 3. Calculate the Sharpe ratio for DIA (assume a risk-free rate of 0). 4. Compare the Sharpe ratio of our mean reversion strategy with that of DIA. 5. Print a message indicating whether our strategy outperformed the general Dow Jones based on the Sharpe ratios. |
The AI generates the following code:
# Import yfinance library to fetch data from Yahoo Finance
import yfinance as yf
# Fetch the daily adjusted close prices for the DIA ETF
dia_data = yf.download('DIA', start=daily_returns.index.min(), end=daily_returns.index.max())['Adj Close']
# Calculate the daily returns for DIA
dia_returns = dia_data.pct_change().dropna()
# Calculate annualized return for DIA
dia_annualized_return = (1 + dia_returns.mean())**252 - 1
# Calculate annualized volatility for DIA
dia_annualized_vol = dia_returns.std() * np.sqrt(252)
# Calculate Sharpe ratio for DIA (assuming a risk-free rate of 0)
dia_sharpe_ratio = dia_annualized_return / dia_annualized_vol
print(dia_sharpe_ratio)
# Compare the Sharpe ratio of our mean reversion strategy with that of DI
if sharpe_ratio > dia_sharpe_ratio:
print("Our mean reversion strategy outperformed the Dow Jones.")
else:
print("Our mean reversion strategy didn't outperform the Dow Jones.")
Step 6: Compare our mean reversion strategy’s performance to that of the Dow Jones ETF
To better understand the performance of our mean reversion strategy compared to investing in the Dow Jones, we will visualize the annual returns, standard deviations, and Sharpe ratios of both strategies. Let’s break down these metrics and why they are relevant to this analysis:
- Annualized return: The average annual return of an investment. It allows for easy comparison of returns across different time frames and investments. We compare the annualized returns of our strategy and the Dow Jones ETF to see which generated higher returns on average.
- Annualized volatility: A measure of the dispersion of returns around the average return. Higher volatility indicates greater risk. Comparing the annualized volatility of our strategy and the Dow Jones ETF shows which had more stable returns.
- Sharpe ratio: A risk-adjusted performance measure comparing excess return to volatility. It reveals whether returns are due to smart decisions or excessive risk. A higher Sharpe ratio indicates better risk-adjusted returns. We compare the Sharpe ratios to determine which offered better returns relative to risk.
Examining these metrics side by side provides insights into the risk-return characteristics of our strategy and the Dow Jones ETF, allowing us to assess whether our strategy can outperform the market on a risk-adjusted basis.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to print the mean reversion strategy’s annual return, annual standard deviation, and Sharpe ratio side by side with the DIA. Nicely display which strategy had the higher risk-adjusted returns as measured by the Sharpe ratio. |
The AI generates the following code:
# Create a DataFrame to hold performance metrics for both strategies
performance_metrics = pd.DataFrame({
'Strategy': ['Mean Reversion', 'Dow Jones'],
'Annualized Return': [annualized_return, dia_annualized_return],
'Annualized Volatility': [annualized_vol, dia_annualized_vol],
'Sharpe Ratio': [sharpe_ratio, dia_sharpe_ratio]
})
# Print the DataFrame
print(performance_metrics)
# Compare Sharpe ratios to determine which strategy had the higher risk-adjusted returns
if sharpe_ratio > dia_sharpe_ratio:
print("The mean reversion strategy had the higher risk-adjusted returns.")
else:
print("The Dow Jones had the higher risk-adjusted returns.")
Backtesting results:
| Strategy | Annualized return | Annualized volatility | Sharpe ratio |
| Mean Reversion | 0.159030 | 0.199897 | 0.795561 |
| Dow Jones | 0.131168 | 0.173794 | 0.754731 |
The results of our analysis show that the mean reversion strategy outperformed the Dow Jones ETF in terms of both annualized returns and risk-adjusted returns. The mean reversion strategy generated higher annual returns while also achieving a higher Sharpe ratio, indicating that it provided better returns relative to the risk taken compared to the Dow Jones ETF.
Step 7: Visualize portfolio growth
To better understand the performance of our mean reversion strategy compared to investing in the Dow Jones, let’s visualize the growth of a hypothetical $100,000 portfolio over time for both strategies.
We can use the following prompt to generate the code for this step:
| Prompt |
| Write Python code to: 1. Calculate the cumulative returns for both our mean reversion strategy and the DIA ETF. 2. Multiply the cumulative returns by the initial investment of $100,000 to get the daily portfolio values for both strategies. 3. Create a beautiful interactive plot using Plotly to visualize the growth of the $100,000 portfolio over time for both our mean reversion strategy and the DIA ETF. 4. Include proper axis labels, a title, and a legend. 5. Display the plot. |
The AI generates the following code:
# Calculate the cumulative returns for our mean reversion strategy and the DIA ETF
capital_over_time['Capital_Returns'] = capital_over_time['Capital'].pct_change() + 1
dia_cumulative_returns = (dia_data.pct_change() + 1).cumprod()
# Multiply the cumulative returns by the initial investment of $100,000 to get the daily portfolio values
capital_over_time['Portfolio_Value'] = capital_over_time['Capital_Returns'].cumprod() * 100000
dia_portfolio_value = dia_cumulative_returns * 100000
# Create the plot using Plotly
import plotly.graph_objects as go
fig = go.Figure()
fig.add_trace(go.Scatter(
x = capital_over_time.index,
y = capital_over_time['Portfolio_Value'],
mode = 'lines',
name = 'Mean Reversion Strategy'
))
fig.add_trace(go.Scatter(
x = capital_over_time.index,
y = dia_portfolio_value,
mode = 'lines',
name = 'DIA ETF'
))
# Include proper axis labels, a title, and a legend
fig.update_layout(
title = "Growth of $100,000 portfolio: Mean Reversion Strategy vs DIA ETF",
xaxis_title = "Date",
yaxis_title = "Portfolio Value ($)",
legend_title = "Strategy",
height = 600,
width = 900,
font = dict(
size = 12
)
)
# Display the plot
fig.show()
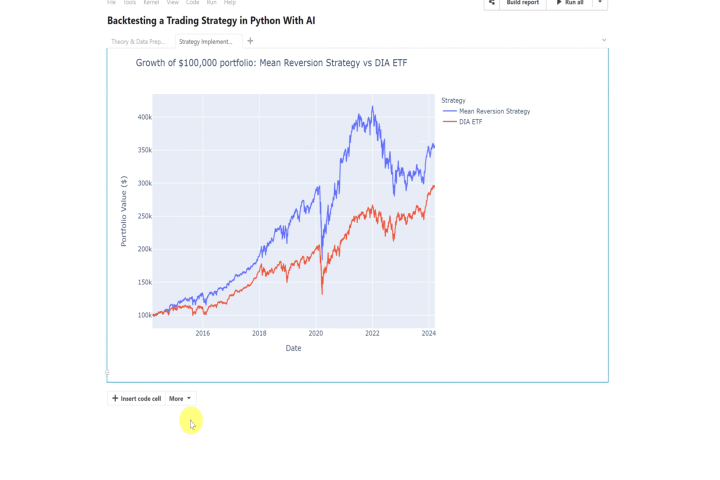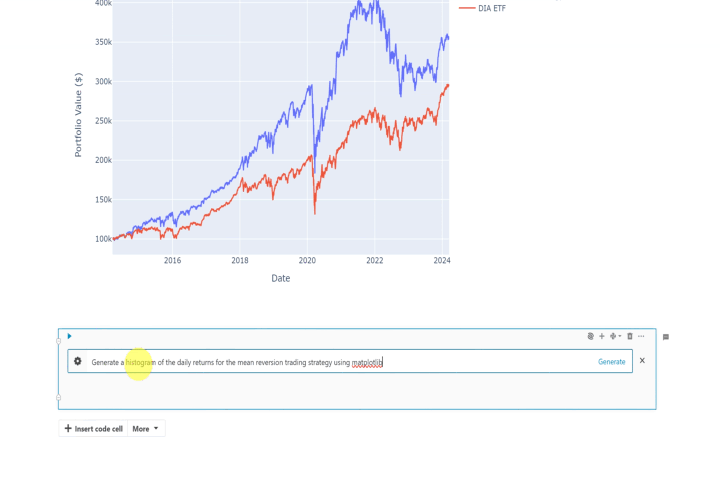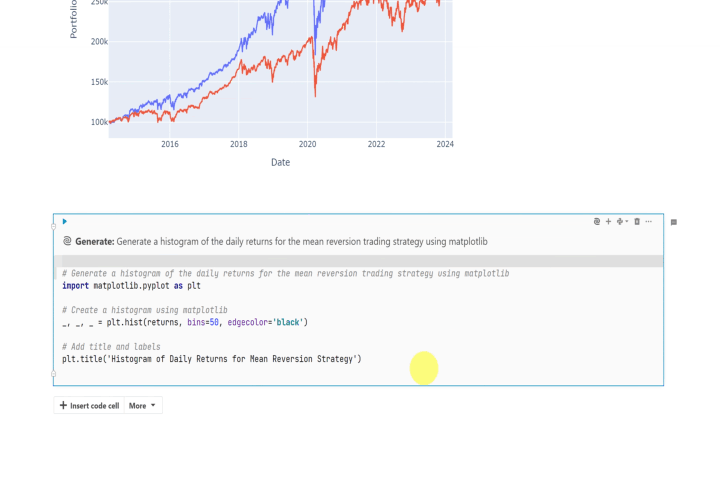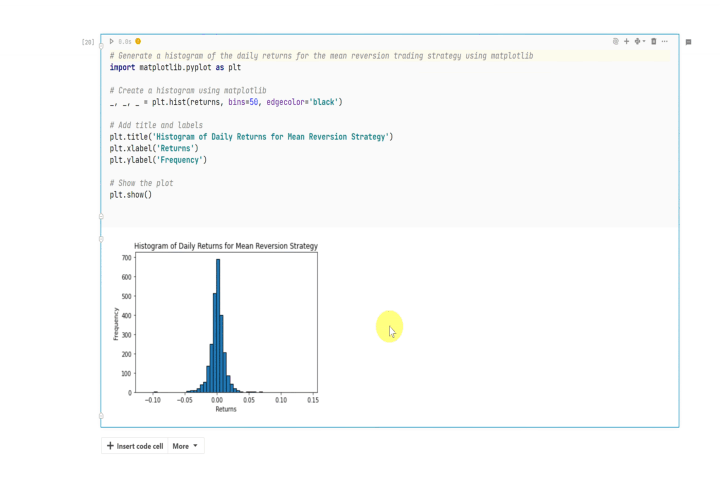
When we run the code, we get the following output:
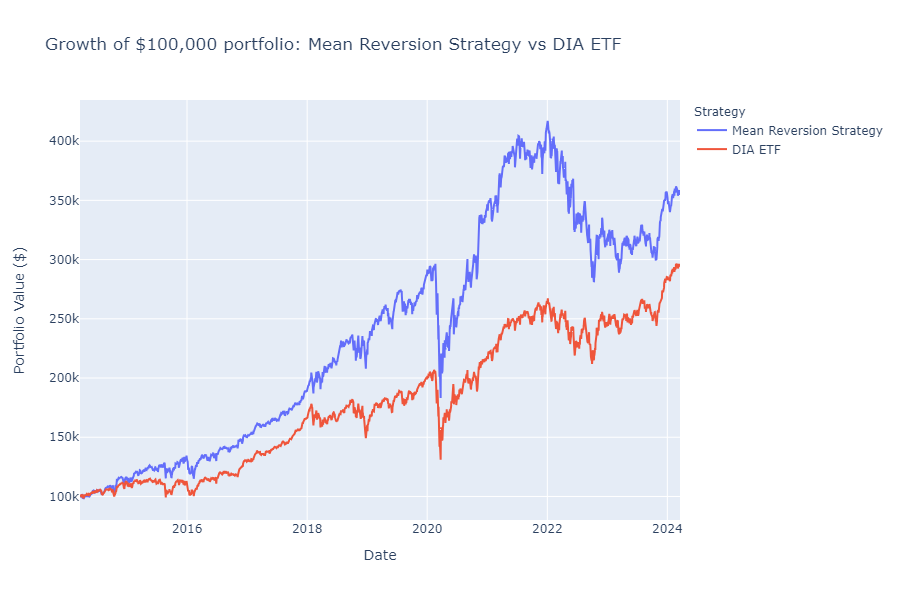
The visualization of the portfolio growth over time provides a clear and compelling illustration of the superior performance of our mean reversion strategy compared to investing in the Dow Jones ETF. Starting with an initial investment of $100,000, the mean reversion strategy’s portfolio value grew to over $350,000 by the end of the 10-year period, demonstrating a significant return on investment.
In contrast, the portfolio value of the Dow Jones ETF, represented by the DIA, only reached a level below $300,000 over the same time frame. This stark difference in portfolio growth highlights the potential of the mean reversion strategy to outperform the broader market, as represented by the DJIA.
The divergence in portfolio values between the two strategies is particularly evident in the later years of the analysis, where the mean reversion strategy’s portfolio continues to climb at a faster rate compared to the Dow Jones ETF. This observation underscores the mean reversion strategy’s ability to capitalize on short-term overreactions in the market and generate superior returns over the long run.
However, it is essential to note that past performance does not guarantee future results. While historical analysis suggests that the mean reversion strategy has outperformed the Dow Jones ETF, it is crucial for investors to consider their own risk tolerance, financial objectives, and conduct thorough research before making any investment decisions.
Fine-tuning and optimization
While our mean reversion strategy has demonstrated impressive performance compared to the Dow Jones ETF, there are several areas where the analysis could be further refined and optimized:
- Lookback period: In this analysis, we identified the 10 biggest losers based on a single day’s returns. Experimenting with different lookback periods, such as using the average returns over the past 3, 5, or 10 days, could potentially improve the strategy’s performance by filtering out noise and focusing on more significant trends.
- Portfolio rebalancing: Our current strategy equally distributes capital among the 10 biggest losers. Exploring different portfolio weighting schemes, such as weighting stocks based on the magnitude of their losses or their market capitalization, could potentially enhance the strategy’s returns and risk management.
- Risk management: Implementing risk management techniques, such as setting stop-loss orders or dynamically adjusting position sizes based on market volatility, could help mitigate potential drawdowns and improve the strategy’s risk-adjusted returns.
- Transaction costs: Our analysis assumes no transaction costs. Incorporating realistic transaction costs, such as commissions and slippage, would provide a more accurate picture of the strategy’s net performance and help identify potential areas for optimization.
- Utilizing a Python backtesting library: While we implemented the mean reversion strategy from scratch, utilizing a Python backtesting library could streamline the process and provide additional features. Popular python backtesting libraries include Backtrader, which offers a simple and intuitive interface, and Zipline, which provides a comprehensive set of tools for complex strategies. These libraries differ in terms of performance, ease of use, and community support, so it’s essential to evaluate them based on the specific requirements of the backtesting project.
- Data cleaning with Datalore’s interactive tables: Instead of relying on AI to write the correct error handling code, we could leverage Datalore’s interactive tables for data cleaning tasks, such as dropping duplicates and columns. Datalore’s interactive tables make data cleaning easy and intuitive, allowing users to quickly identify and remove duplicates or unnecessary columns with just a few clicks. This feature streamlines the data preparation process and ensures that the data used for backtesting is clean and reliable.
By exploring these areas for fine-tuning and optimization, investors and analysts can further refine the mean reversion strategy and potentially unlock even greater performance potential. However, it’s essential to approach these optimizations with caution and thoroughly backtest any modifications to ensure they are robust and effective across different market conditions.
Conclusion
In conclusion, our exploration of a simple mean reversion strategy using the Dow Jones Industrial Average constituents has yielded compelling results. By leveraging the power of Python and the AI-assisted capabilities of Datalore notebooks, we were able to efficiently backtest the strategy and compare its performance with the broader market.
The results of our analysis demonstrate that the mean reversion strategy, which involves buying the 10 biggest losers in the Dow Jones Index each day and selling them at the close of the following trading day, outperformed the Dow Jones ETF in terms of both annualized returns and risk-adjusted returns. The visualization of the hypothetical portfolio’s growth over time further reinforces the potential of this strategy to generate superior returns compared to simply investing in the market index.
However, it is crucial to emphasize that past performance does not guarantee future results, and investors should always consider their individual risk tolerance and financial goals before implementing any investment strategy. Nonetheless, this exercise serves as a powerful demonstration of how Python, coupled with AI-assisted tools like Datalore, can empower investors and analysts to test and refine trading strategies, ultimately leading to more informed and data-driven investment decisions.
If you would like to see an executive summary of the report in Datalore, you can visit this link.
Subscribe to Datalore News and Updates




