Kotlin
A concise multiplatform language developed by JetBrains
Idiomatic Kotlin: Simulating a console to solve Advent of Code
Today in “Idiomatic Kotlin”, we’re solving another Advent of Code challenge. We will be simulating, diagnosing, and fixing a small, made up game console! If you have ever wanted to implement your own virtual machine or emulator for an existing system like a game console or a retro computing device, you’ll find this issue particularly interesting!
As usual, a number of Kotlin features will help us achieve that goal, like sealed classes, sequences, and immutability.
Understanding the challenge
The story of Advent of Code 2020, Day 8 goes like this:
A passenger on our flight hands us a little retro game console that won’t turn on. It somehow seems to be stuck in an infinite loop, executing the same program over and over again. We want to help them by fixing it!
To do so, we first need to run a simulation of the program on our own. At a later point, we want to fix the console so that it no longer gets stuck in a loop. Because the input for this challenge contains a lot of information, we’ll spend some time dissecting it together.
The input for our challenge is a bunch of instructions, which are executed by the gaming device. If you’ve ever delved into how computers work, you might recognize this as some kind of “Assembly Language” – essentially simple low-level instructions for a processor that are executed one after the other, top down, without all the fancy bells and whistles that higher-level languages offer:

By looking through the code and the problem description, we can identify three different types of instructions: nop, jmp, and acc, which always come with a numeric value. We can use the industry standard terms to refer to the parts of an instruction. The first part (nop / jmp / acc) is called the “opcode”. The second part of the instruction is called the “immediate value”.
Our problem statement gives us some hints about how to interpret the combination of opcodes and immediate values.
- The
nop(No Operation) instruction doesn’t do anything besides advance to the following instruction. We can also ignore its immediate value for the time being. - The
jmp(Jump) instruction jumps a given number of instructions ahead or back, based on its immediate value. - The
acc(Accumulator) instruction modifies the only real memory of our little device, its “accumulator” register, which can save the result of additions or subtractions, again based on the immediate value that follows.
Based on this understanding of the input for our challenge, we can make some deductions that help us model the machine in Kotlin.
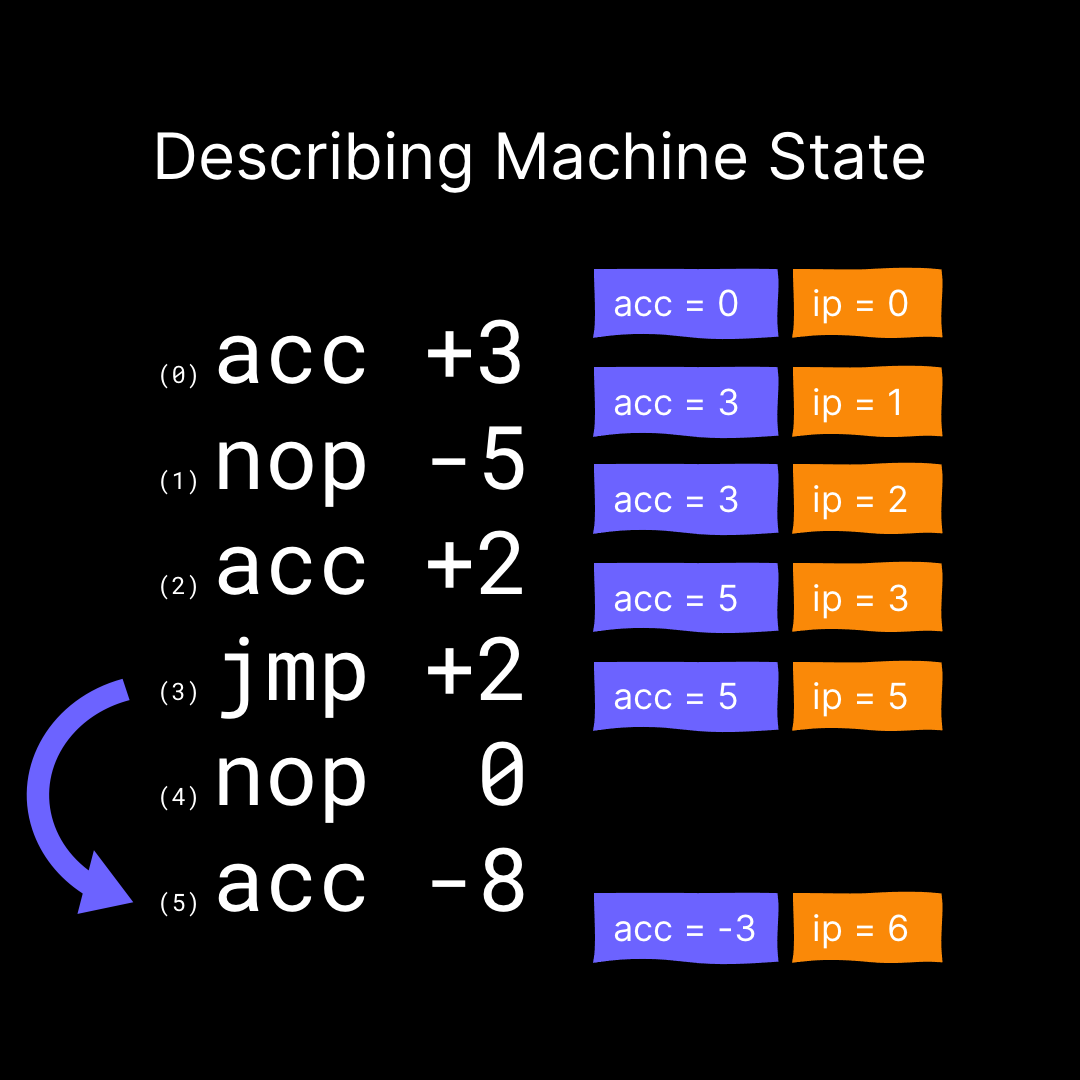
The first one of those is that the current state of the machine can be fully described with two numbers:
- The accumulator, which is the result of any calculations that we’ve made so far.
- The index for the next instruction that we want to execute. In computing, this is called the “instruction pointer” or “program counter”.
This graphic shows that indeed, the only moving parts in our machine are the accumulator and the instruction pointer. For a step-by-step walkthrough, be sure to watch the video accompanying this blog post.
The second observation is that instructions behave just like functions that take an accumulator and instruction pointer as inputs and return a new accumulator and instruction pointer as outputs. This graphic shows how the acc instruction acts like a function, but the same applies for the nop and jmp instructions, as well:

We are now armed with the knowledge we need to actually implement a simulator for this device. To recap:
- The input for our program is a number of instructions in a list (the “program”)
- Each instruction in our program can modify two things:
- The instruction pointer, which determines the next instruction to be executed
- The accumulator, which stores a single number
- Our device continuously reads the instruction and executes it based on its current state. This process continues until we end up with an instruction pointer that is outside the bounds of our program, indicating termination.
Building a device simulator
With our understanding of the puzzle input, let’s move on to what we need in order to successfully run the program we’re given as a puzzle input. Because we’re told this program is stuck in some kind of loop, the actual “answer” to the challenge is going to be the value of the accumulator immediately before we execute an instruction a second time.
Before we even think about how to detect loops in such a program, let’s start by building a small simulator for the device.
Modeling the machine and its instructions
The first step is to model the machine’s state and its instructions. We determined that the state of the machine can be fully described using two numbers: the instruction pointer and the accumulator. We can model this pair as an immutable data class:
We then need to define the three different types of instructions that the machine understands. To do so, let’s create a small class hierarchy to represent the different types of instructions. This will allow us to share some attributes across all instructions and distinguish between the different types of instructions that we may encounter.
Because we figured out that an instruction can take a machine state and return a new machine state, we will attach an action attribute to all instructions. The action attribute is a function that transforms one machine state into a new one:
We also mark the Instruction class as sealed, allowing us to create subclasses for it and ensuring that the compiler is aware of all the subclasses for our Instruction class.
The first subclass we can tackle is the nop instruction. As per its name (“No Operation”), it does nothing but move on to the next instruction. Expressed in terms of the action associated with this instruction, it creates a new MachineState with an instruction pointer that is incremented by one. The accumulator remains unchanged. We can use the typical lambda syntax here to define our “action” function. It receives the previous MachineState as the implicitly named parameter it.
Because all nop instructions behave the same, we can use the object keyword to create a singleton object for them, instead of creating a whole class for this instruction:
The next instruction is the jmp instruction. We recall that the behavior of the jmp instruction only changes the instruction pointer, because that’s the part of the machine state that determines what instruction to run next. How far ahead or back the jump goes is determined by the attached immediate value – the accumulator once again remains unchanged:
Lastly, we implement the acc instruction, which adds its immediate value to the accumulator and increments the instruction pointer so that the program continues running with the next instruction:
Executing programs
With this model for state and instructions in place, we can move on to running a list of instructions, one after the other – a whole program.
Let’s write up a function called execute, which does exactly that: It starts the device with an initial state, where both instruction pointer and accumulator are zero. It performs a loop for as long as our instruction pointer is valid. Inside the loop, we read the instruction at the current index from our list. We then apply the action that is associated with that instruction, and feed it the current state of the machine. This returns a new state of the machine, from which we can continue execution. We can also add a quick call to println to ensure that this code actually runs as we expect it to.
If the program behaves correctly, then at some point the instruction pointer should go out of bounds – indicating that the program terminated. In this case, we can return the latest state of the machine. This would be our “happy path”. The finished function looks like this:
To see if the function actually works, let’s also add the functionality required to read our program from the input text file. If you’ve followed along with the series, you probably already have a good idea of how we approach this: We open the file, read all of the lines of text inside, and turn them into Instruction objects by applying the map function.
Of course, we also need to actually figure out what kind of Instruction objects we actually want. To do so, we can write a small factory function, that does two things:
- It uses the
splitfunction to turn the full lines into the instruction names and their associated value - It uses a
whenstatement to instantiate the appropriate class – eithernop,acc, orjmp
Note that this is one of the few situations where the Kotlin style guide expressly allows us to start a function with an uppercase letter. What we’re writing here is a “factory function”, which is intentionally allowed to look similar to a constructor call.
With these helper functions added to our program, we are ready to run it, passing the list of instructions we just parsed to the execute function:
When we run the program, we quickly notice that it does not terminate. This makes sense – our challenge was to find where our program begins infinitely looping and to see what the last machine state is exactly before we enter the loop a second time. But – at the very least – we have confirmed that something really is wrong with the input code for our challenge!
Detecting cycles and solving part 1
We can easily retrofit a simple kind of cycle detection into our execute function. To figure out when we see an instruction for the second time, we keep track of each instruction index we’ve encountered so far and save it in a Set. Whenever we’re done executing an instruction, we check whether our new instruction pointer contains a value that we’ve seen before. This would indicate that an instruction will be executed for a second time, meaning we can just return the current state of the machine:
Running our simulator again, our program successfully detects the loop, and returns the last machine state before the cycle would continue. We enter the accumulator value as returned by the function on adventofcode.com, and celebrate our first star for this challenge! ⭐
Solving part 2
In the second part of the challenge, we go beyond just finding an error, and try our hand at fixing the program we’ve been presented. We receive an important hint in the problem statement: exactly one instruction is the root cause for the infinite loop. Somewhere in the long list of instructions, one of the jmp instructions is supposed to be a nop instruction, or vice versa.
We can apply a rather straightforward approach to attempt a solution. To find out which instruction needs fixing, we generate all possible versions of the program where a nop has been exchanged with a jmp and the other way around. We can then run them all and see whether any of them terminate.
We can apply a small optimization here and base our solution on Kotlin’s sequences, which allow us to do the same calculations, but in a lazy manner. By using sequences, our code will only generate those adjusted programs that we actually need, until we’ve found a working version, and then it will terminate. Essentially, we create a mutated program, execute it, and see whether it terminates. If it doesn’t, we create the next mutation and run the check again.
We can write a function called generateAllMutations, which takes the original program as its input and returns a sequence of other program codes that have been modified. Each element of that sequence will be a full program, but with one instruction exchanged.
We use the sequence builder to create a “lazy collection” of programs, by creating working copies of the original program and exchanging the appropriate instructions at the correct indices. Instead of returning a list of programs at the end, we “yield” an individual value. That is, we hand over a value to the consumer of our sequence. When our program hits this point, our code here actually stops doing work – until the next value in the sequence is requested, at which point we run the next iteration of our loop. The whole function looks like this:
To make this code work, we need to make some adjustments to the model of our machine instructions. We now know that we need the immediate values of nop operations in order to generate the corresponding jmp instructions. Thus, we turn the nop object back into a full class with its very own immediate value:
This also requires a small change in the Instruction factory function, so that it properly parses the immediate value:
To obtain our second star, we now feed our original program to the generateAllMutations function, and execute the sequence of new, altered programs using the map function. At this point, we have another sequence, this time of the results of the programs.
Because we’re only interested in the first one where the instruction pointer went outside of the instructions of our program, we use the first function with a predicate that expresses exactly that. This is also the so-called terminal operation of our chain of sequences. It turns a value from our sequence into the actual MachineState as returned by the execute function.
In a way, we have actually benefited from the fact that we just built a basic simulator first without caring too much about the detection of endless loops. Because we assumed that some programs might terminate, we handled that “happy path” correctly from the beginning. That just made it easier to get our second star by running our main function once more and submitting the last state of the machine before it terminates!
Performance considerations
Before we rest on our laurels, we can revisit our code a little more and talk about the implicit decisions that we made. One of the key factors that comes to mind with our implementation is its trade-off between immutability vs performance.
Maybe without realizing it, we’ve adopted an approach for defining and executing instructions that creates a lot of objects. Specifically, each time the action associated with an Instruction is invoked, a new MachineState object is created. This approach has pros and cons:
- Generally speaking, using immutability like this can make it much easier to reason about your system. You don’t need to worry that somewhere, some code will change the internal state of the objects that you are referencing. While that may not apply here, it can become a really big deal, especially if your program uses concurrency (coroutines or threads). So it’s worth considering an approach like this from the get-go.
- However, we’re also paying a price by allocating so many objects. For a small simulation like the one we have here, this approach is still possible, even when the task requires us to run like 600 modified programs. But if you’re writing a simulator for a real retro gaming device, or just any machine that can store more than a few numbers, this approach isn’t really applicable. Imagine having to copy the whole content of your machine’s RAM every time your CPU executes an instruction – you can probably see why that wouldn’t work.
One opinion on the topic that’s certainly worth reading is that of Kotlin Team Lead Roman Elizarov. He actually published an article called “Immutability we can afford”, where he talks about this. If you’re conscientious about how you’re architecting and optimizing your software, you might find this a compelling read.
A mutable implementation
To get a better understanding of the difference between an immutable and a mutable implementation, we can write a second version of the simulator, allowing us to examine some very basic performance characteristics.
Instead of completely rewriting the whole project, we can introduce a new executeMutably function with the same signature as our original execute function. The key difference in its implementation is the way the instruction pointer and accumulator are stored as mutable variables. This implementation also uses a when statement instead of relying on the action associated with an Instruction, which would always allocate a new MachineState:
From an outside perspective, this function behaves exactly like the original execute function. We can validate this by adding calls to it to our main function. We can also wrap these function calls in invocations of measureTimedValue. This is an experimental function in the Kotlin standard library that can measure how long it takes for the block that it is passed to execute, and also return the original return value of that block:
The measurements that we can obtain using this of course have obvious flaws: we only run the process once, and don’t take into account things like JVM warmup time and other factors that might influence the performance of our code. While both implementations terminate within a pretty reasonable timeframe, we are indeed paying a price when we use the version which makes heavy use of immutability:
If we wanted to perform more detailed and reliable measurements, we would be better off using a framework like kotlinx.benchmark. However, even these basic numbers can give us an idea of the magnitude in performance difference between the two implementations.
At the end of the day, performance considerations like this will ultimately be up to you. Programming is a game of trade-offs, and choosing one of these implementations is another one of them.
Wrapping up
In today’s issue, we’ve gone through a lot of thinking, coding, and problem solving! Let’s quickly recap what we saw today:
- We saw how we can use sealed classes and lambdas to represent the instructions of our simulated device, making sure the compiler always looks over our shoulder and ensures that we handle all instructions correctly, even when creating alternative versions of our input program.
- We built a basic run cycle for our simulator, making sure we modified the machine state according to the instructions we received. We used Kotlin sets to discover loops in the execution of those input programs.
- We used sequences and the
sequencebuilder function to construct a lazy collection of programs for our second challenge. We also saw how we would yield those sequence elements on demand. - Lastly, we took some performance metrics into consideration, evaluating a different approach for executing the program and doing some armchair benchmarking using the experimental
measureTimedValuefunction.
Many of these topics are worth diving a little deeper into, and we’re also planning on covering many of them in future videos on our official channel. So, subscribe to our YouTube channel and hit the bell to receive notifications when we continue the Kotlin journey!
As usual, we’d like to say thanks to the folks behind Advent of Code, specifically Eric Wastl, who gave us permission to use the Advent of Code problem statements for this series. Check out adventofcode.com, and continue puzzling on your own.
Subscribe to Kotlin Blog updates







