Detección de anomalías en series temporales

¿Cómo identificar patrones inusuales en los datos que puedan revelar problemas críticos u oportunidades ocultas? La detección de anomalías ayuda a identificar los datos que se desvían significativamente de la norma. Los datos de series temporales, que constan de datos recogidos a lo largo del tiempo, suelen incluir tendencias y patrones estacionales. Las anomalías en los datos de series temporales se producen cuando se interrumpen estos patrones, lo que convierte a la detección de anomalías en una valiosa herramienta en sectores como las ventas, las finanzas, la fabricación y la atención sanitaria.
Dado que los datos de series temporales tienen características únicas como la estacionalidad y las tendencias, se requieren métodos especializados para detectar anomalías de forma eficaz. En este artículo del blog, exploraremos algunos métodos populares para la detección de anomalías en series temporales, incluyendo la descomposición STL y la predicción LSTM, con ejemplos de código detallados para ayudarle a empezar.
Detección de anomalías en series temporales en las empresas
Los datos de series temporales son esenciales para muchas empresas y servicios. Muchas empresas registran los datos a lo largo del tiempo con marcas de tiempo, lo que permite analizar los cambios y comparar los datos a lo largo del tiempo. Las series temporales son útiles cuando se compara una cantidad determinada a lo largo de un periodo determinado, como, por ejemplo, en una comparación interanual en la que los datos presentan características de estacionalidad.
Seguimiento de las ventas
Uno de los ejemplos más comunes de datos de series temporales con estacionalidad son los datos de ventas. Dado que muchas ventas se ven afectadas por las fiestas anuales y la época del año, es difícil sacar conclusiones sobre los datos de ventas sin tener en cuenta la estacionalidad. Por ello, un método habitual para analizar y detectar anomalías en los datos de ventas es la descomposición STL, que trataremos en detalle más adelante en este artículo del blog.
Finanzas
Los datos financieros, como las transacciones y los precios de las acciones, son ejemplos típicos de datos de series temporales. En el sector financiero, analizar y detectar anomalías en estos datos es una práctica habitual. Por ejemplo, los modelos de predicción de series temporales pueden utilizarse en el trading automático. Utilizaremos una predicción de series temporales para identificar anomalías en los datos bursátiles más adelante en este artículo del blog.
Fabricación
Otro caso de uso de la detección de anomalías en series temporales es la supervisión de defectos en las líneas de producción. Las máquinas suelen supervisarse, lo que permite disponer de datos de series temporales. Es esencial poder notificar a la dirección los posibles fallos, y la detección de anomalías desempeña un papel clave.
Medicina y sanidad
En medicina y sanidad, se controlan las constantes vitales humanas y se pueden detectar anomalías. Esto ya es importante en la investigación médica, pero es fundamental en el diagnóstico. Si un paciente de un hospital presenta anomalías en sus constantes vitales y no se le trata inmediatamente, los resultados pueden ser fatales.
¿Por qué es importante utilizar métodos especiales para la detección de anomalías en las series temporales?
Los datos de series temporales son especiales en el sentido de que a veces no pueden tratarse como otros tipos de datos. Por ejemplo, cuando aplicamos una división entrenamiento-prueba a datos de series temporales, a causa de la naturaleza secuencialmente relacionada de los datos, no podemos cambiarlos de orden. Esto también sucede cuando se aplican datos de series temporales a un modelo de aprendizaje profundo. Se suele utilizar una red neuronal recurrente (RNN) para tener en cuenta la relación secuencial, y los datos de entrenamiento se introducen como ventanas temporales, que conservan la secuencia de acontecimientos en su interior.
Los datos de series temporales también son especiales porque a menudo presentan estacionalidad y tendencias que no podemos ignorar. Esta estacionalidad puede manifestarse en un ciclo de 24 horas, un ciclo de 7 días o un ciclo de 12 meses, por nombrar algunas posibilidades comunes. Las anomalías solo pueden determinarse después de haber tenido en cuenta la estacionalidad y las tendencias, como verá en nuestro ejemplo a continuación.
Métodos utilizados para la detección de anomalías en las series temporales
Dado que los datos de series temporales son especiales, existen métodos específicos para detectar anomalías en ellos. Dependiendo del tipo de datos, algunos de los métodos y algoritmos que mencionamos en el anterior artículo del blog sobre detección de anomalías pueden utilizarse en datos de series temporales. Sin embargo, con esos métodos, la detección de anomalías puede no ser tan robusta como si se utilizaran los diseñados específicamente para datos de series temporales. En algunos casos, puede utilizarse una combinación de métodos de detección para reconfirmar el resultado de la detección y evitar falsos positivos o negativos.
Descomposición STL
Una de las formas más populares de utilizar datos de series temporales que presentan estacionalidad es la descomposición STL: descomposición de la tendencia estacional mediante LOESS (regresión local). En este método, una serie temporal se descompone utilizando una estimación de la estacionalidad (con el periodo proporcionado o determinado mediante un algoritmo), una tendencia (estimada) y el residuo (el ruido de los datos). Una biblioteca Python que proporciona herramientas de descomposición STL es la biblioteca statsmodels.
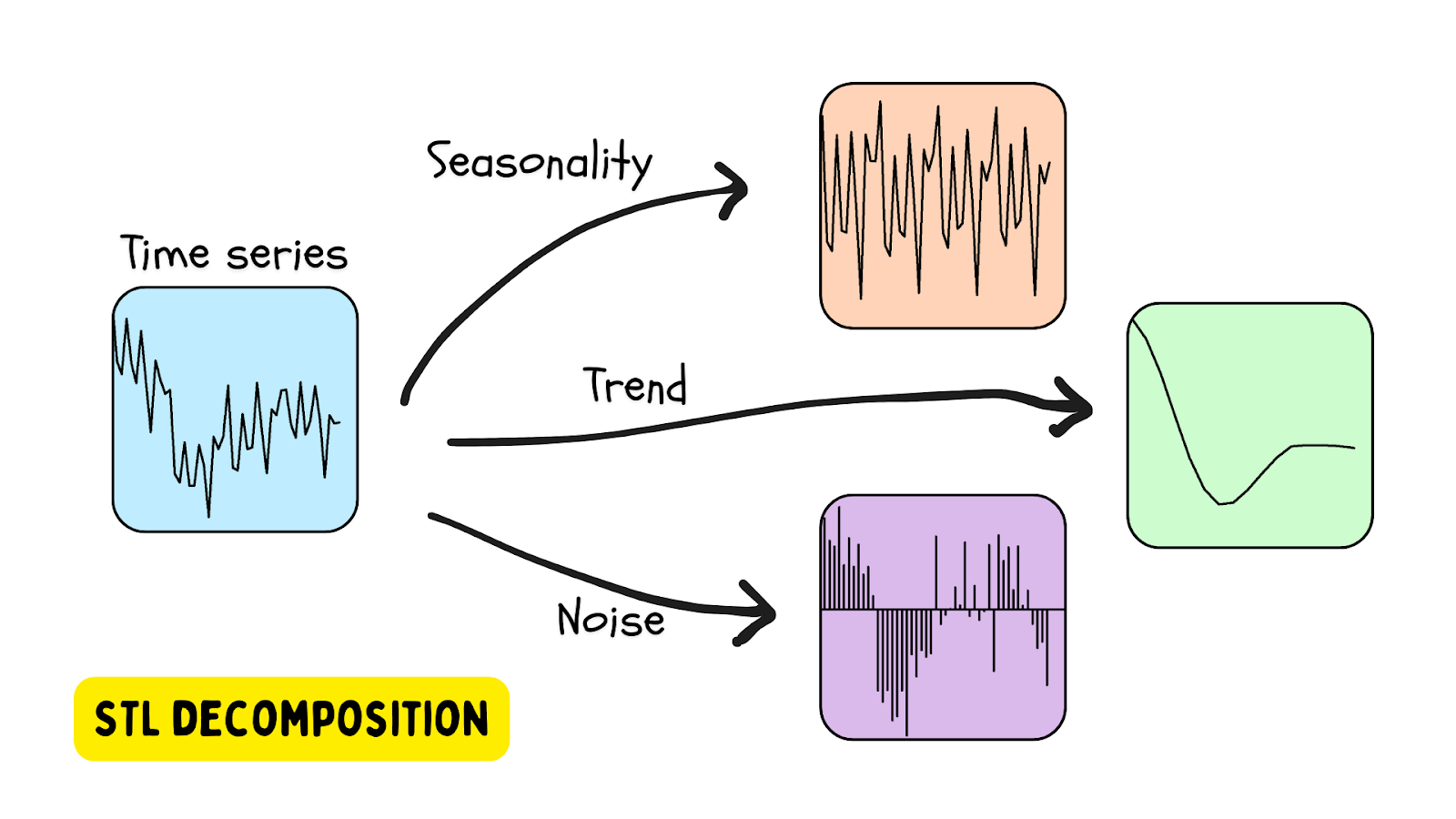
Se detecta una anomalía cuando el residuo supera un determinado umbral.
Uso de la descomposición STL en los datos de una colmena
En un artículo del blog anterior, exploramos la detección de anomalías en colmenas utilizando OneClassSVM y los métodos IsolationForest.
En este tutorial, analizaremos datos de colmenas como una serie temporal utilizando la clase STL proporcionada por la biblioteca statsmodels. Para empezar, configure su entorno utilizando este archivo: requierements.txt.
1. Instale la biblioteca
Dado que solo hemos estado utilizando el modelo proporcionado por Scikit-learn, necesitaremos instalar statsmodels desde PyPI. Esto es fácil de hacer en PyCharm.
Vaya a la ventana Python Packages (elija el icono de la parte inferior izquierda del IDE) y escriba statsmodels en el cuadro de búsqueda.
Puede ver toda la información sobre el paquete en la parte derecha. Para instalarlo, solo tiene que hacer clic en Install package.
2. Cree un notebook de Jupyter
Para investigar más a fondo el conjunto de datos, vamos a crear un notebook de Jupyter para aprovechar las herramientas que proporciona el entorno de notebooks de Jupyter de PyCharm.
Importaremos pandas y cargaremos el archivo .csv.
import pandas as pd
df = pd.read_csv('../data/Hive17.csv', sep=";")
df = df.dropna()
df
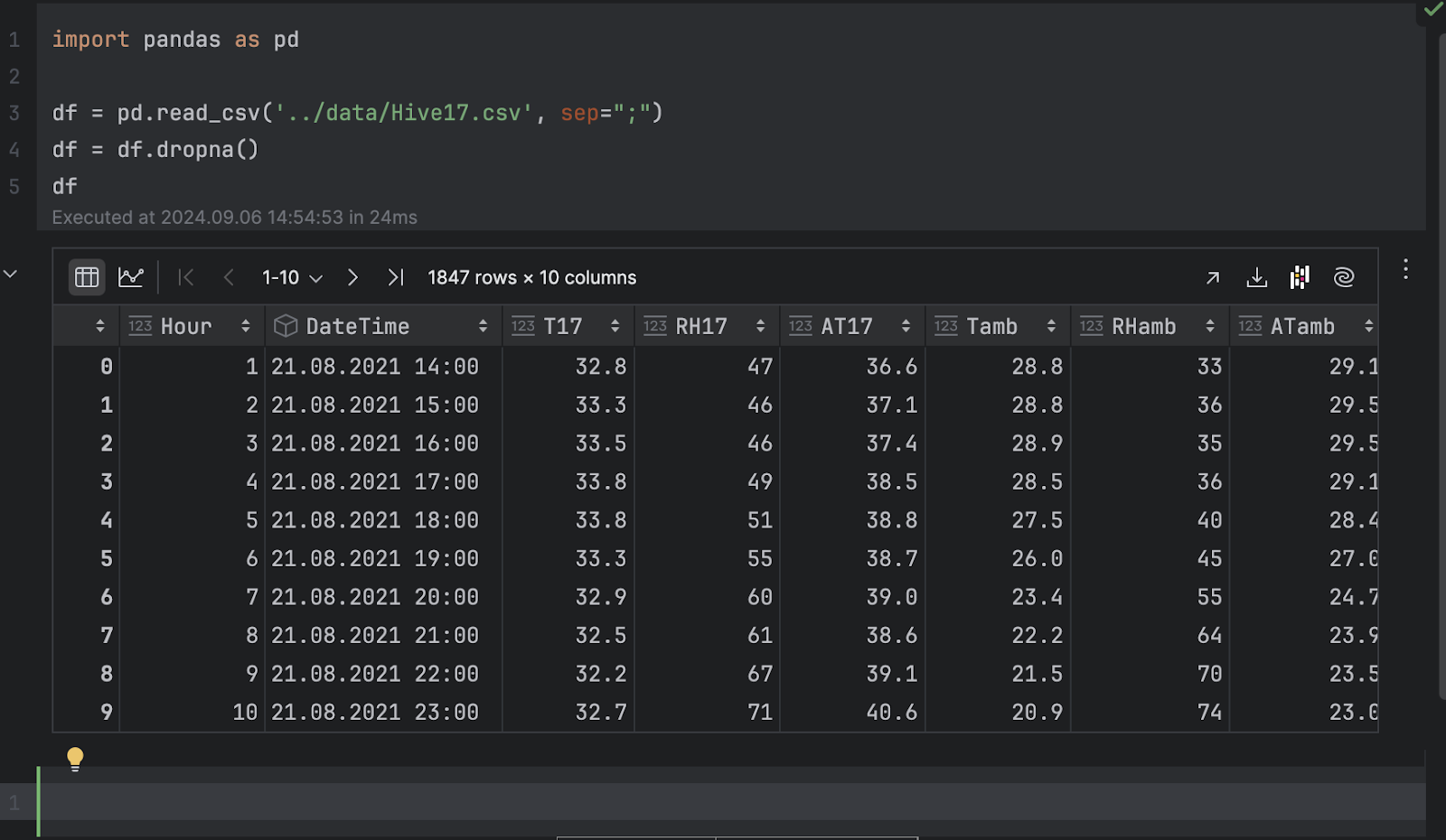
3. Inspeccione los datos en forma de gráficos
Ahora, podemos inspeccionar los datos en forma de gráficos. Aquí nos gustaría ver la temperatura de la colmena 17 a lo largo del tiempo. Haga clic en Chart view en el inspector del marco de datos y, a continuación, elija T17 como eje y en los ajustes de la serie.
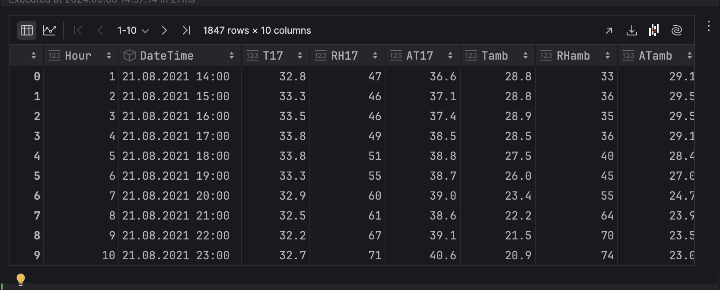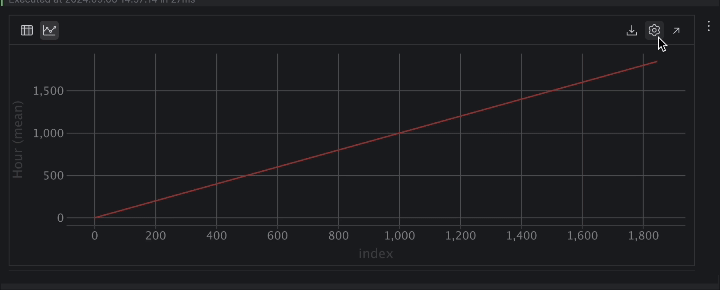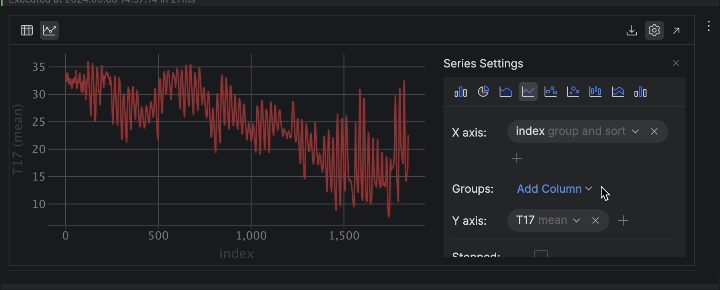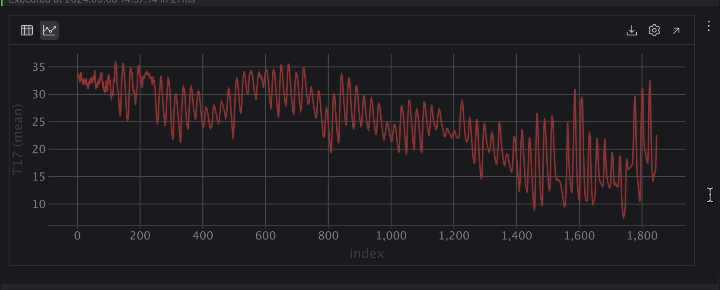
Cuando se expresa como una serie temporal, la temperatura presenta muchos altibajos. Esto indica un comportamiento periódico, probablemente debido al ciclo día-noche, por lo que podemos asumir con seguridad que existe un periodo de 24 horas para la temperatura.
A continuación, se observa una tendencia a la baja de la temperatura con el paso del tiempo. Si inspecciona la columna DateTime, podrá ver que las fechas van de agosto a noviembre. Dado que la página Kaggle del conjunto de datos indica que los datos se recopilaron en Turquía, la transición del verano al otoño explica nuestra observación de que la temperatura desciende con el tiempo.
4. Descomposición de series temporales
Para comprender las series temporales y detectar anomalías, realizaremos una descomposición STL, importando la clase STL de statsmodels y ajustándola con nuestros datos de temperatura.
from statsmodels.tsa.seasonal import STL stl = STL(df["T17"], period=24, robust=True) result = stl.fit()
Tendremos que indicar un periodo para que la descomposición funcione. Como hemos mencionado antes, es seguro asumir un ciclo de 24 horas.
Según la documentación, STL descompone una serie temporal en tres componentes: tendencia, estacional y residual. Para obtener una visión más clara del resultado descompuesto, podemos utilizar el método incorporado plot:
result.plot()
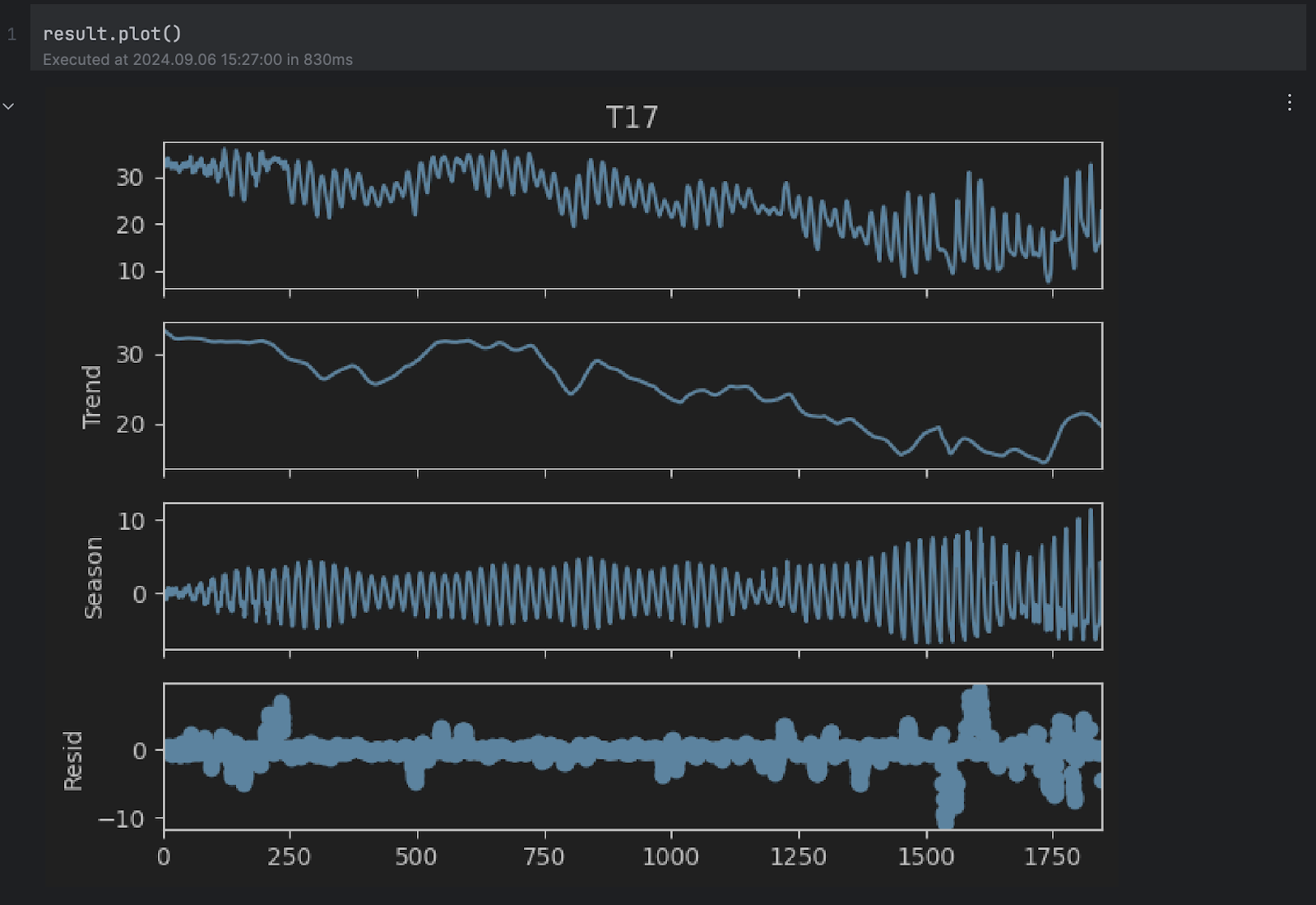
Puede ver que los gráficos Trend y Season parecen alinearse con nuestras suposiciones anteriores. Sin embargo, nos interesa el gráfico residual de la parte inferior, que es la serie original sin la tendencia ni los cambios estacionales. Cualquier valor extremadamente alto o bajo en el residuo indica una anomalía.
5. Umbral de anomalía
A continuación, nos gustaría determinar qué valores del residuo consideraremos anómalos. Para ello, podemos observar el histograma del residuo.
result.resid.plot.hist()
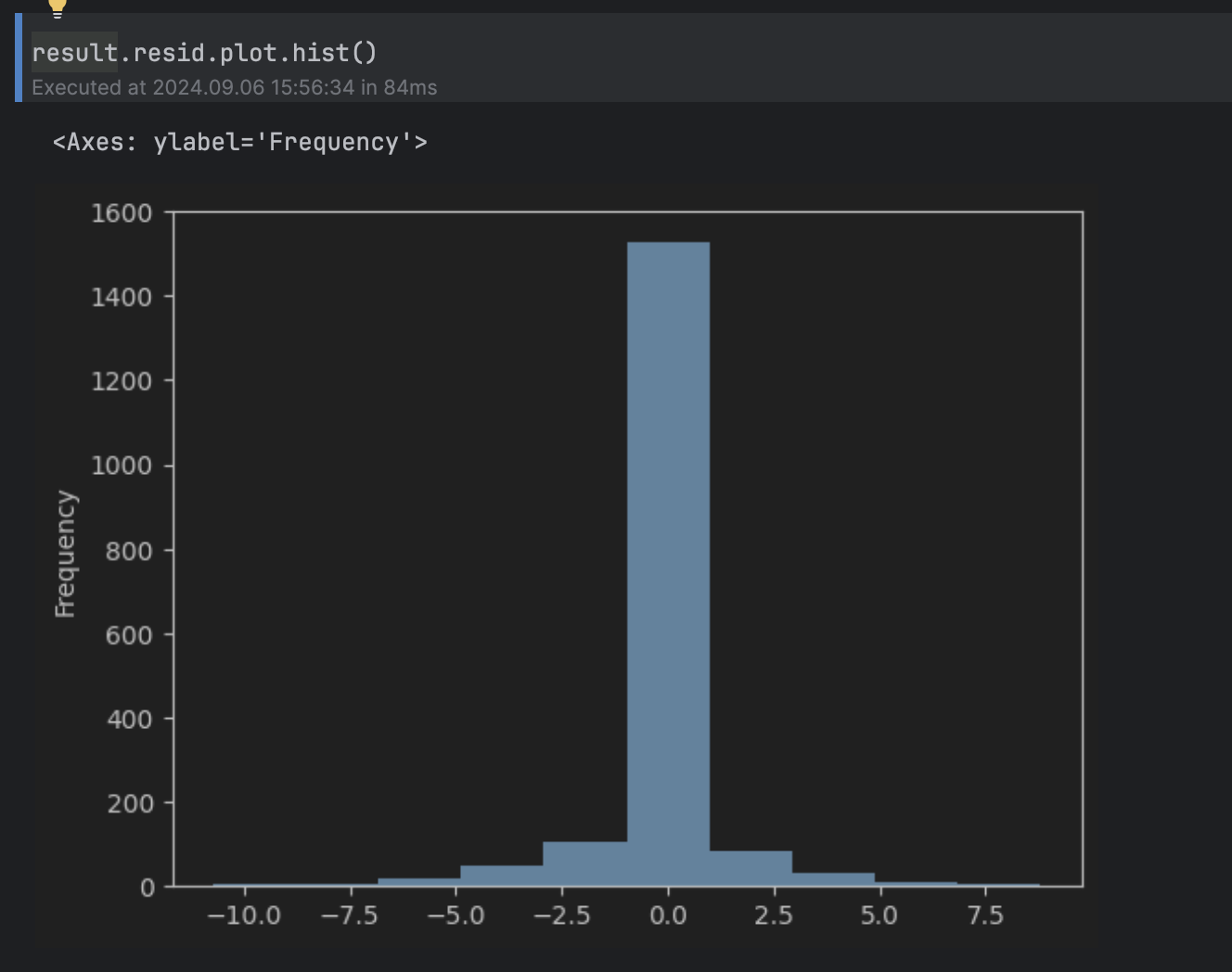
Esta puede considerarse una distribución normal en torno a 0, con una larga cola por encima de 5 y por debajo de -5, por lo que fijaremos el umbral en 5.
Para mostrar las anomalías en la serie temporal original, podemos colorearlas todas de rojo en el gráfico de esta forma:
import matplotlib.pyplot as plt
threshold = 5
anomalies_filter = result.resid.apply(lambda x: True if abs(x) > threshold else False)
anomalies = df["T17"][anomalies_filter]
plt.figure(figsize=(14, 8))
plt.scatter(x=anomalies.index, y=anomalies, color="red", label="anomalies")
plt.plot(df.index, df['T17'], color='blue')
plt.title('Temperatures in Hive 17')
plt.xlabel('Hours')
plt.ylabel('Temperature')
plt.legend()
plt.show()
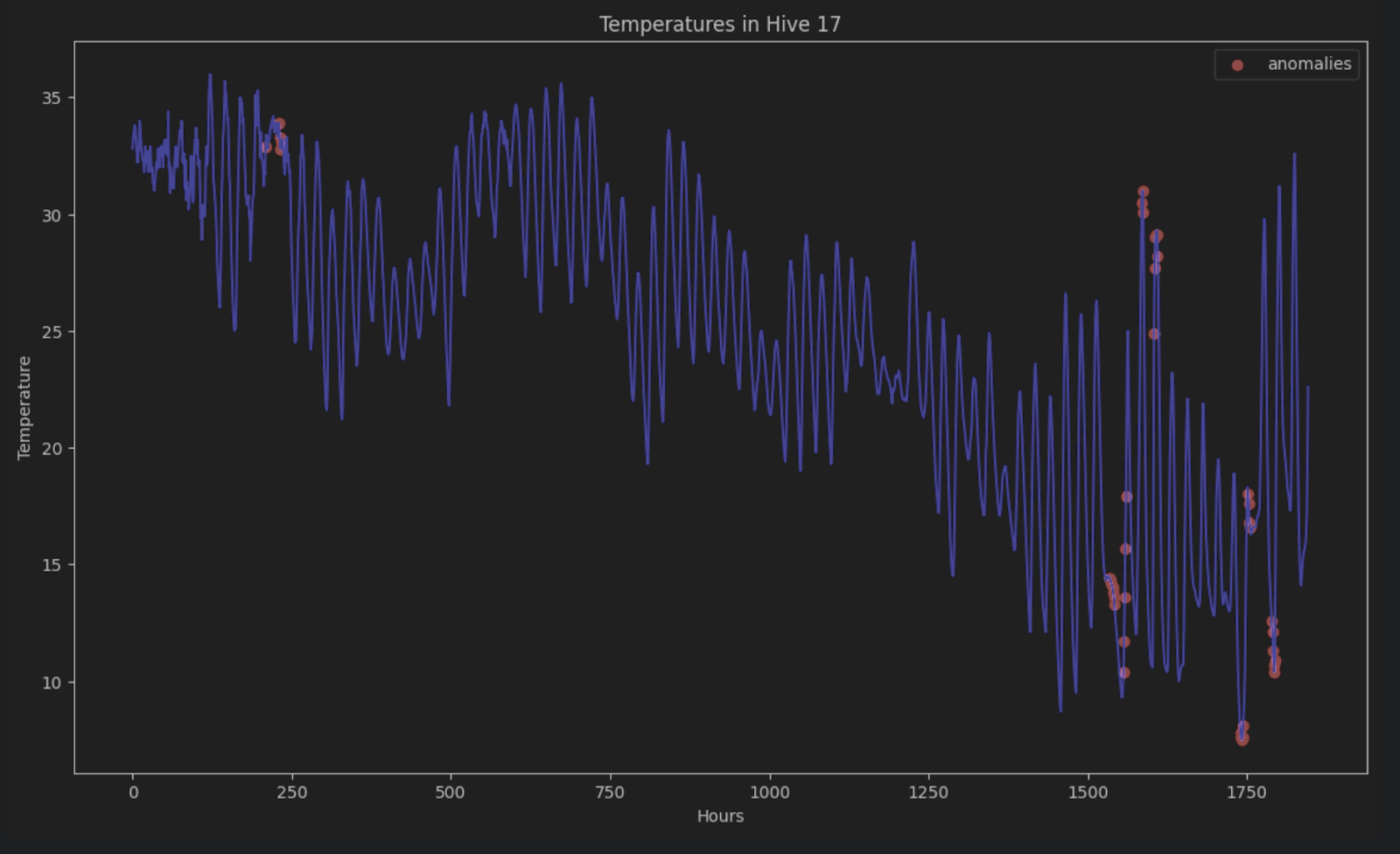
Sin la descomposición STL, es muy difícil identificar estas anomalías en una serie temporal formada por periodos y tendencias.
Predicción LSTM
Otra forma de detectar anomalías en los datos de series temporales es realizar una predicción de las series temporales sobre las series utilizando métodos de aprendizaje profundo para estimar el resultado de los puntos de datos. Si una estimación es muy diferente del punto de datos real, podría ser un signo de datos anómalos.
Uno de los algoritmos de aprendizaje profundo más populares para realizar la predicción de datos secuenciales es el modelo de memoria a largo plazo (LSTM), que es un tipo de red neuronal recurrente (RNN). El modelo LSTM tiene puertas de entrada, olvido y salida, que son matrices numéricas. Esto garantiza que la información importante se transmita en la siguiente iteración de los datos.
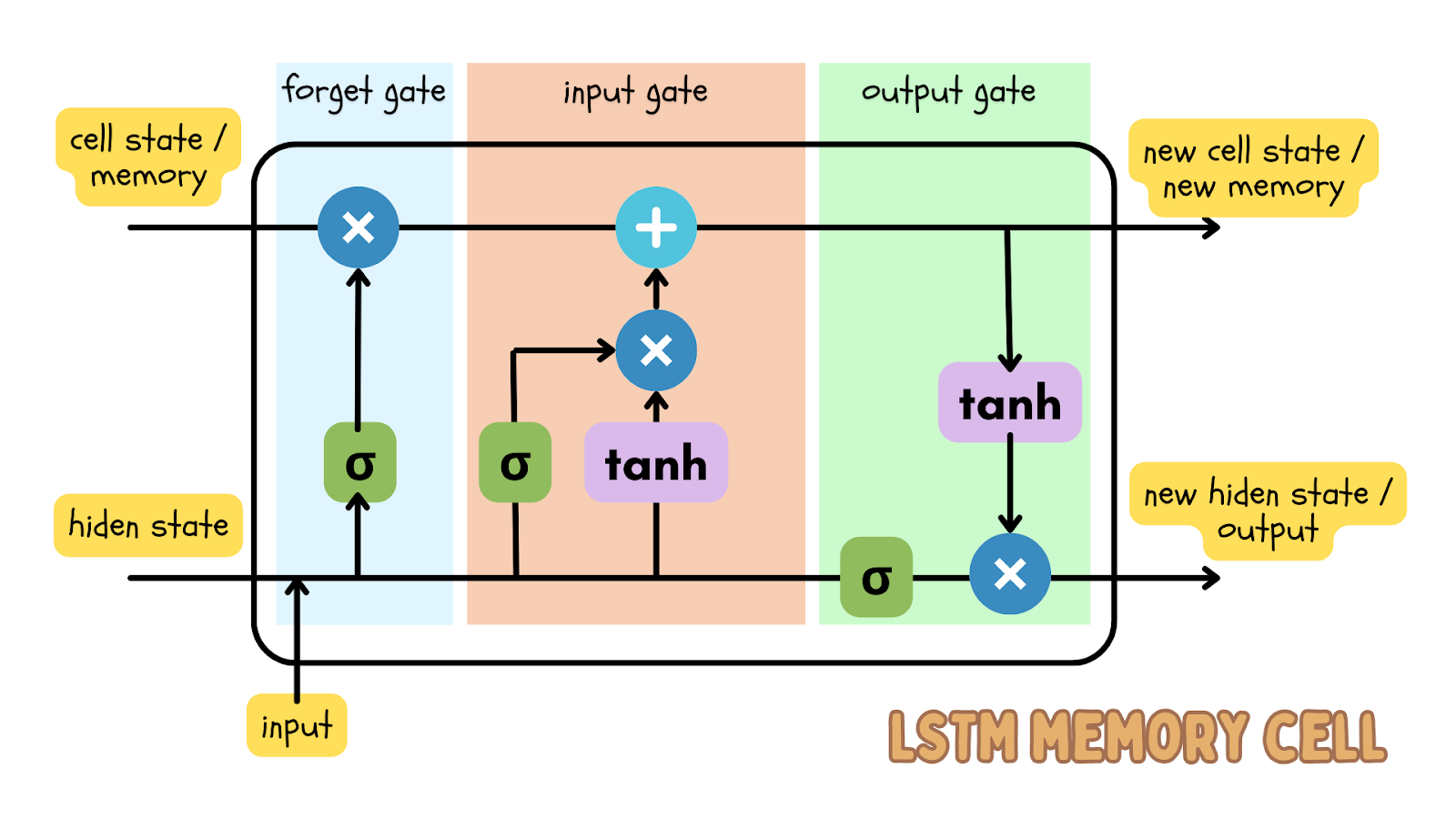
Dado que los datos de series temporales son datos secuenciales —lo que significa que el orden de los puntos de datos es secuencial y no deben modificarse— el modelo LSTM es un modelo de aprendizaje profundo eficaz para predecir el resultado en un momento determinado. Esta predicción puede compararse con los datos reales y puede fijarse un umbral para determinar si los datos reales son una anomalía.
Uso de la predicción LSTM en las cotizaciones bursátiles
Ahora vamos a iniciar un nuevo proyecto Jupyter para detectar cualquier anomalía en el precio de las acciones de Apple durante los últimos 5 años. El conjunto de datos sobre cotizaciones bursátiles muestra los datos más actualizados. Si desea seguir el artículo del blog, puede descargar el conjunto de datos que estamos utilizando.
1. Inicie un proyecto de Jupyter
Al iniciar un nuevo proyecto, puede optar por crear uno de Jupyter, que está optimizado para la ciencia de datos. En la ventana New Project, puede crear un repositorio Git y determinar qué instalación de conda utilizar para gestionar su entorno.
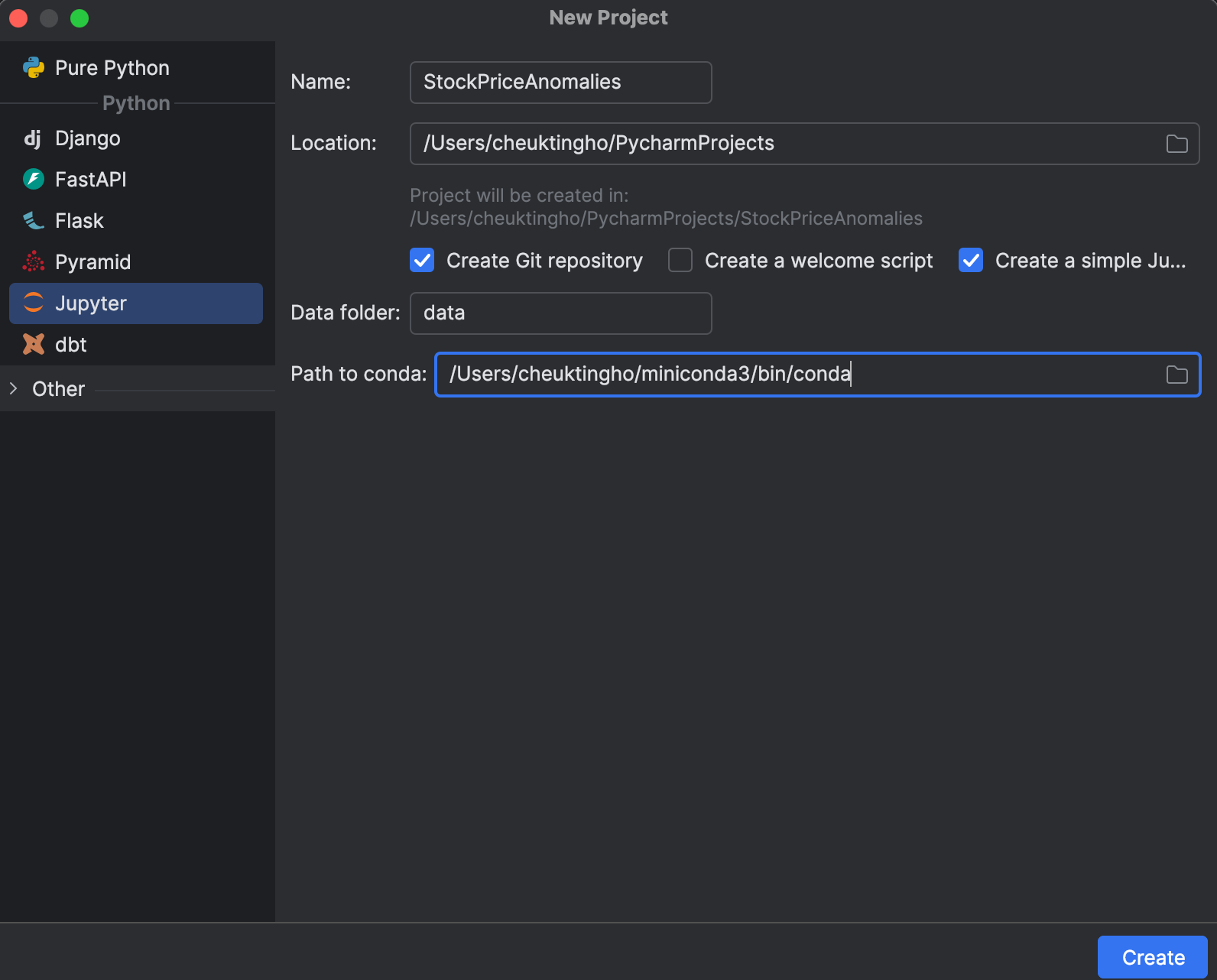
Tras iniciar el proyecto, verá un notebook de ejemplo. Inicie un nuevo notebook de Jupyter para este ejercicio.
A continuación, vamos a configurar requirements.txt. Necesitaremos pandas, matplotlib y PyTorch, cuyo nombre es torch en PyPI. Como PyTorch no está incluido en el entorno conda, PyCharm nos dirá que nos falta el paquete. Para instalar el paquete, haga clic en la bombilla y seleccione Install all missing packages.
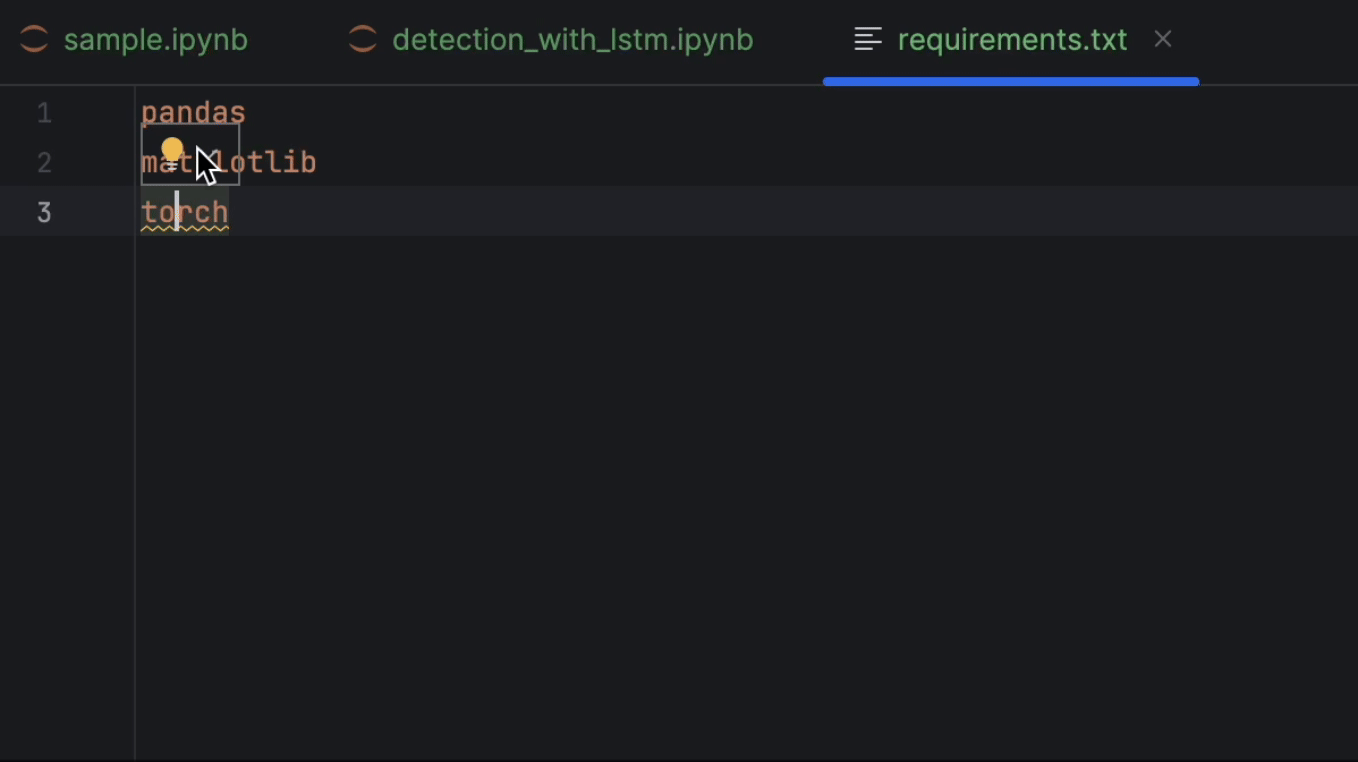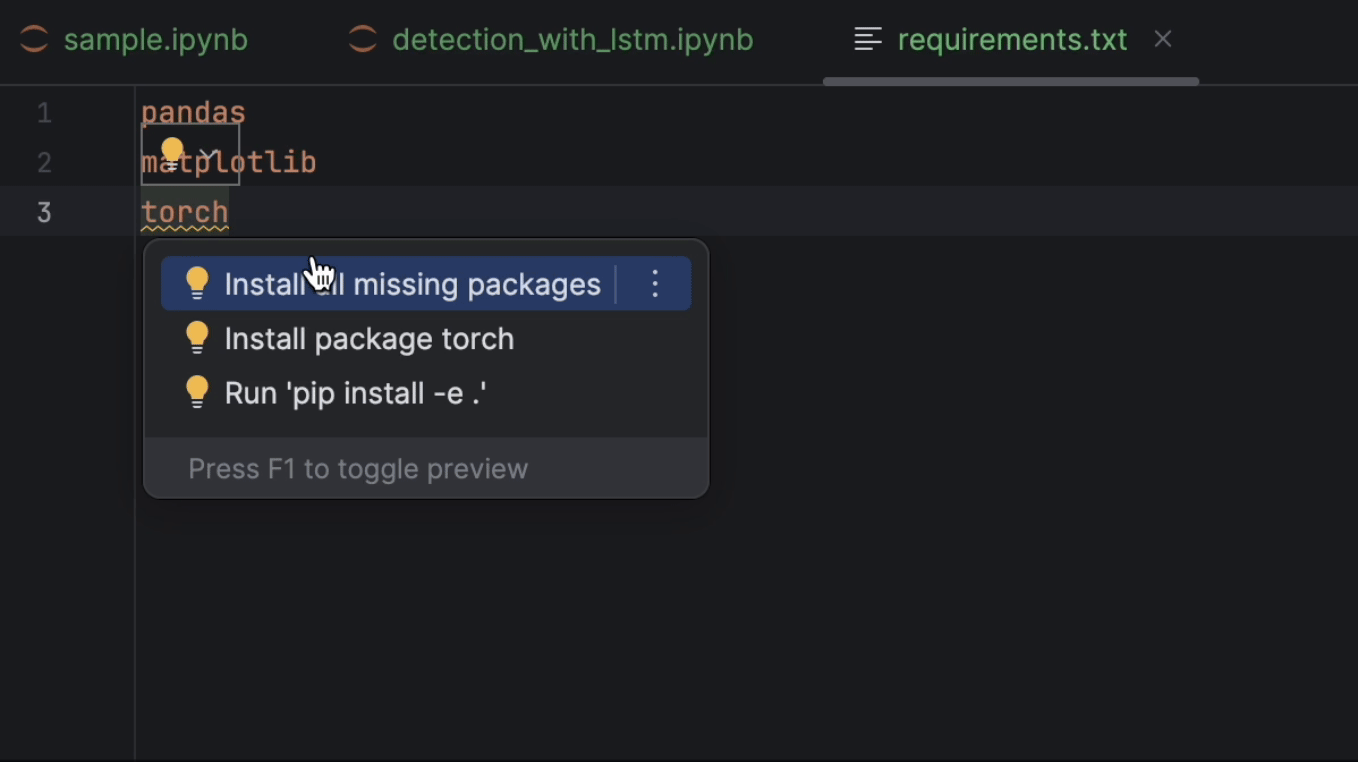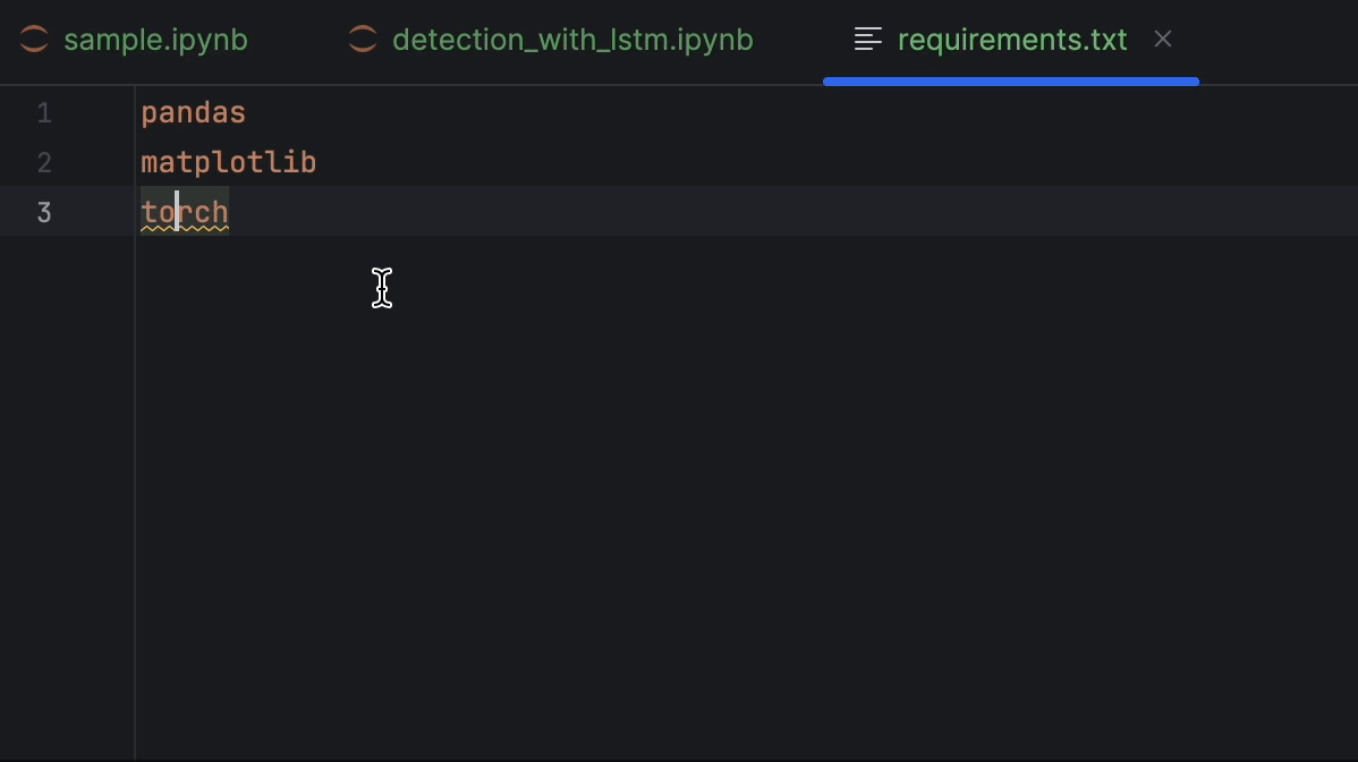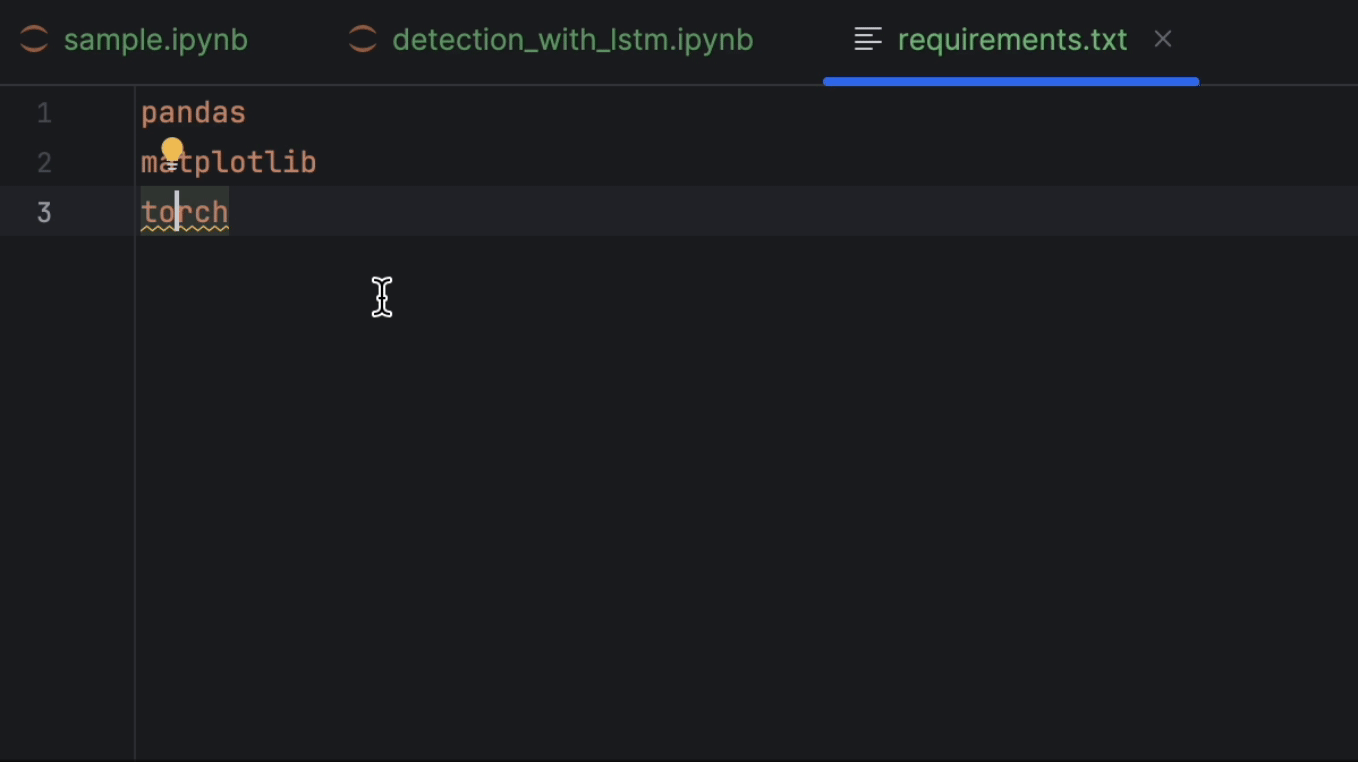
2. Carga e inspección de los datos
A continuación, pongamos nuestro conjunto de datos apple_stock_5y.csv en la carpeta de datos y carguémoslo como un DataFrame de pandas para inspeccionarlo.
import pandas as pd
df = pd.read_csv('data/apple_stock_5y.csv')
df
Con la tabla interactiva, podemos ver fácilmente si falta algún dato.
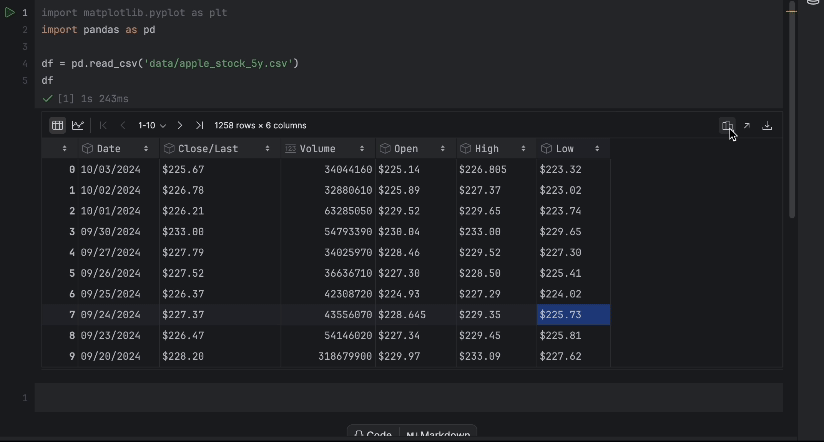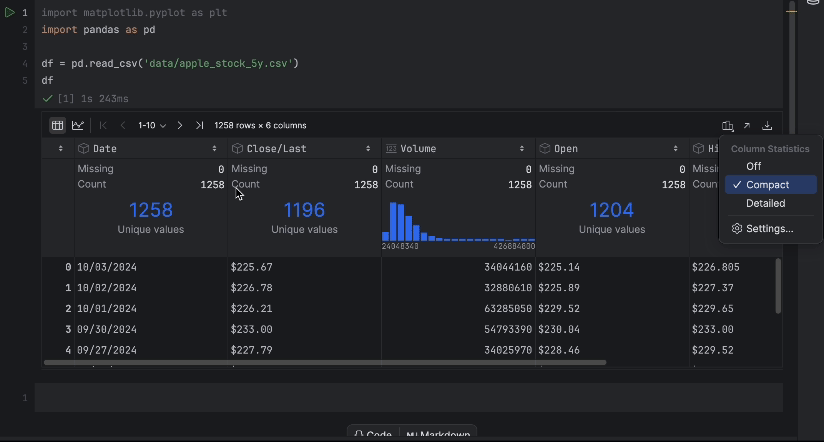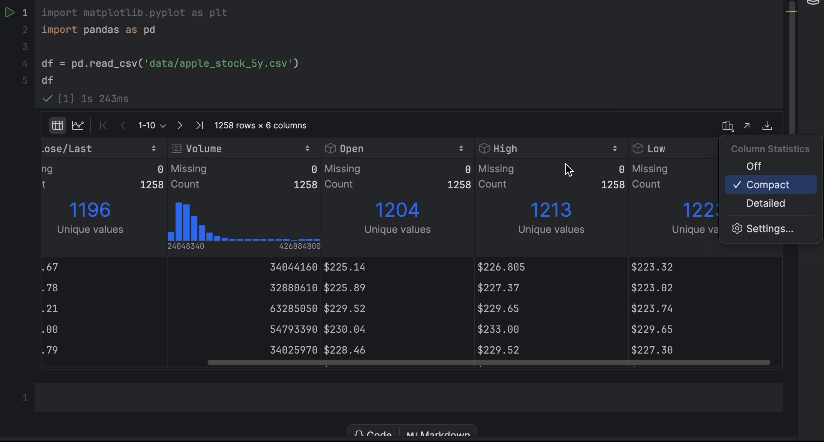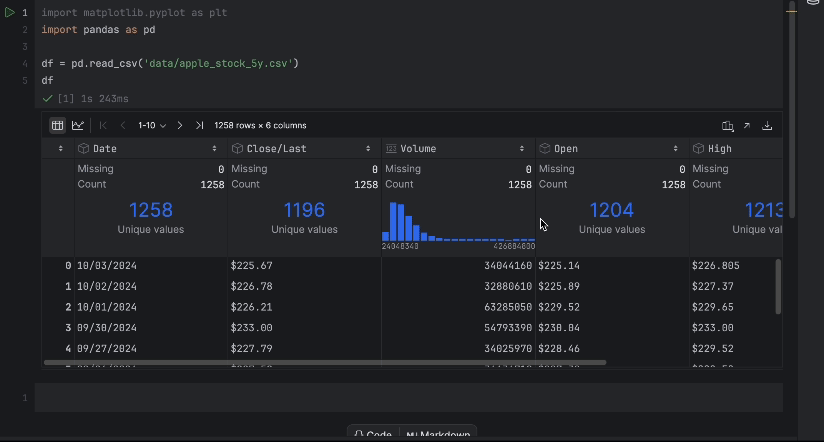
No faltan datos, pero tenemos un problema: nos gustaría utilizar el precio Close/Last<, pero no es un tipo de dato numérico. Hagamos una conversión e inspeccionemos de nuevo nuestros datos:
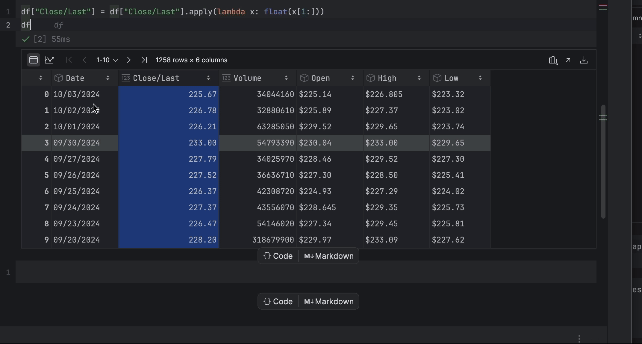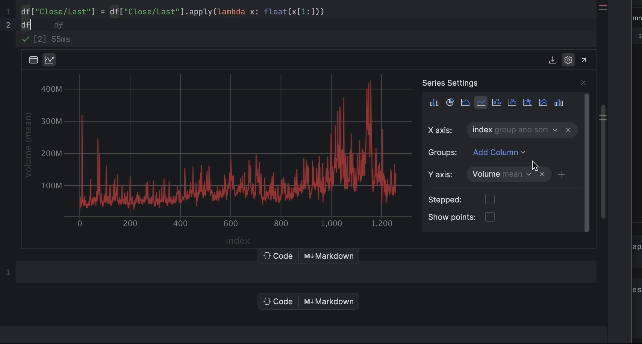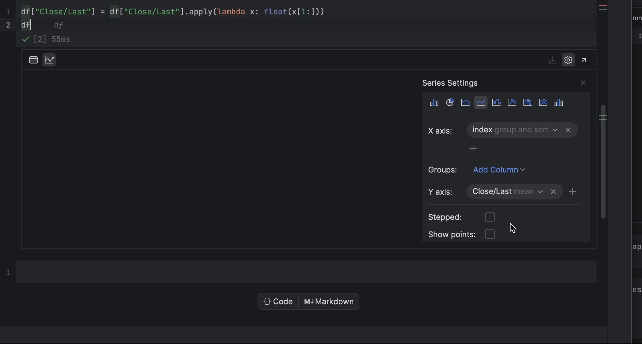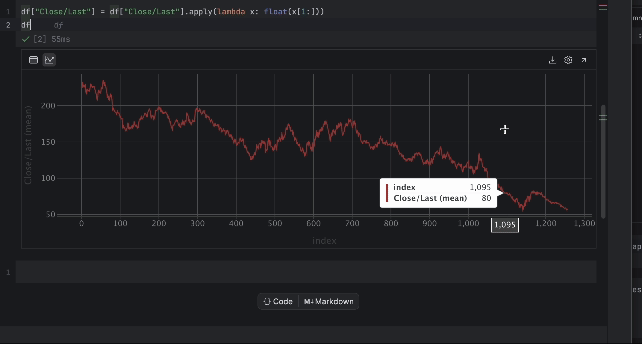
df["Close/Last"] = df["Close/Last"].apply(lambda x: float(x[1:])) df
Ahora podemos inspeccionar el precio con la tabla interactiva. Haga clic en el icono de gráfico de la izquierda y se creará un gráfico. De forma predeterminada, utiliza Date como eje x y Volume como eje y. Como queremos inspeccionar el precio Close/Last, vaya a la configuración haciendo clic en el icono del engranaje de la derecha y elija Close/Last como eje y.
3. Preparación de los datos de entrenamiento para el modelo LSTM
A continuación, tenemos que preparar los datos de entrenamiento que se utilizarán en el modelo LSTM. Necesitamos preparar una secuencia de vectores (característica X), cada uno de los cuales representa una ventana temporal, para predecir el próximo precio. El siguiente precio formará otra secuencia (objetivo y). Aquí podemos elegir el tamaño de esta ventana de tiempo con la variable lookback. El siguiente código crea secuencias X e Y que más adelante se convertirán en tensores de PyTorch:
import torch
lookback = 5
timeseries = df[["Close/Last"]].values.astype('float32')
X, y = [], []
for i in range(len(timeseries)-lookback):
feature = timeseries[i:i+lookback]
target = timeseries[i+1:i+lookback+1]
X.append(feature)
y.append(target)
X = torch.tensor(X)
y = torch.tensor(y)
print(X.shape, y.shape)
En términos generales, cuanto mayor sea la ventana, mayor será nuestro modelo, ya que el vector de entrada es más grande. Sin embargo, con una ventana mayor, la secuencia de entradas será más corta, por lo que determinar esta ventana de retrospección requiere un gran equilibrio. Empezaremos con 5, pero no dude en probar diferentes valores para ver las diferencias.
4. Cree y entrene el modelo
Podemos crear el modelo generando una clase con el módulo nn en PyTorch antes de entrenarlo. El módulo nn proporciona bloques de construcción, como las diferentes capas de la red neuronal. En este ejercicio, crearemos una sencilla capa LSTM seguida de una capa lineal:
import torch.nn as nn
class StockModel(nn.Module):
def __init__(self):
super().__init__()
self.lstm = nn.LSTM(input_size=1, hidden_size=50, num_layers=1, batch_first=True)
self.linear = nn.Linear(50, 1)
def forward(self, x):
x, _ = self.lstm(x)
x = self.linear(x)
return x
A continuación, entrenaremos nuestro modelo. Antes de entrenarlo, necesitaremos crear un optimizador, una función de pérdida utilizada para calcular la pérdida entre los valores predichos y los reales de y, y un cargador de datos para introducir nuestros datos de entrenamiento:
import numpy as np import torch.optim as optim import torch.utils.data as data model = StockModel() optimizer = optim.Adam(model.parameters()) loss_fn = nn.MSELoss() loader = data.DataLoader(data.TensorDataset(X, y), shuffle=True, batch_size=8)
El cargador de datos puede cambiar el orden de las entradas, puesto que ya hemos creado las ventanas temporales. Esto conserva la relación secuencial en cada ventana.
El entrenamiento se realiza mediante un bucle for que realiza un bucle sobre cada época. Cada 100 épocas, imprimiremos la pérdida y observaremos mientras el modelo converge:
n_epochs = 1000
for epoch in range(n_epochs):
model.train()
for X_batch, y_batch in loader:
y_pred = model(X_batch)
loss = loss_fn(y_pred, y_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 != 0:
continue
model.eval()
with torch.no_grad():
y_pred = model(X)
rmse = np.sqrt(loss_fn(y_pred, y))
print(f"Epoch {epoch}: RMSE {rmse:.4f}")
Comenzamos con 1000 épocas, pero el modelo converge con bastante rapidez. No dude en probar otros números de épocas de entrenamiento para obtener el mejor resultado.
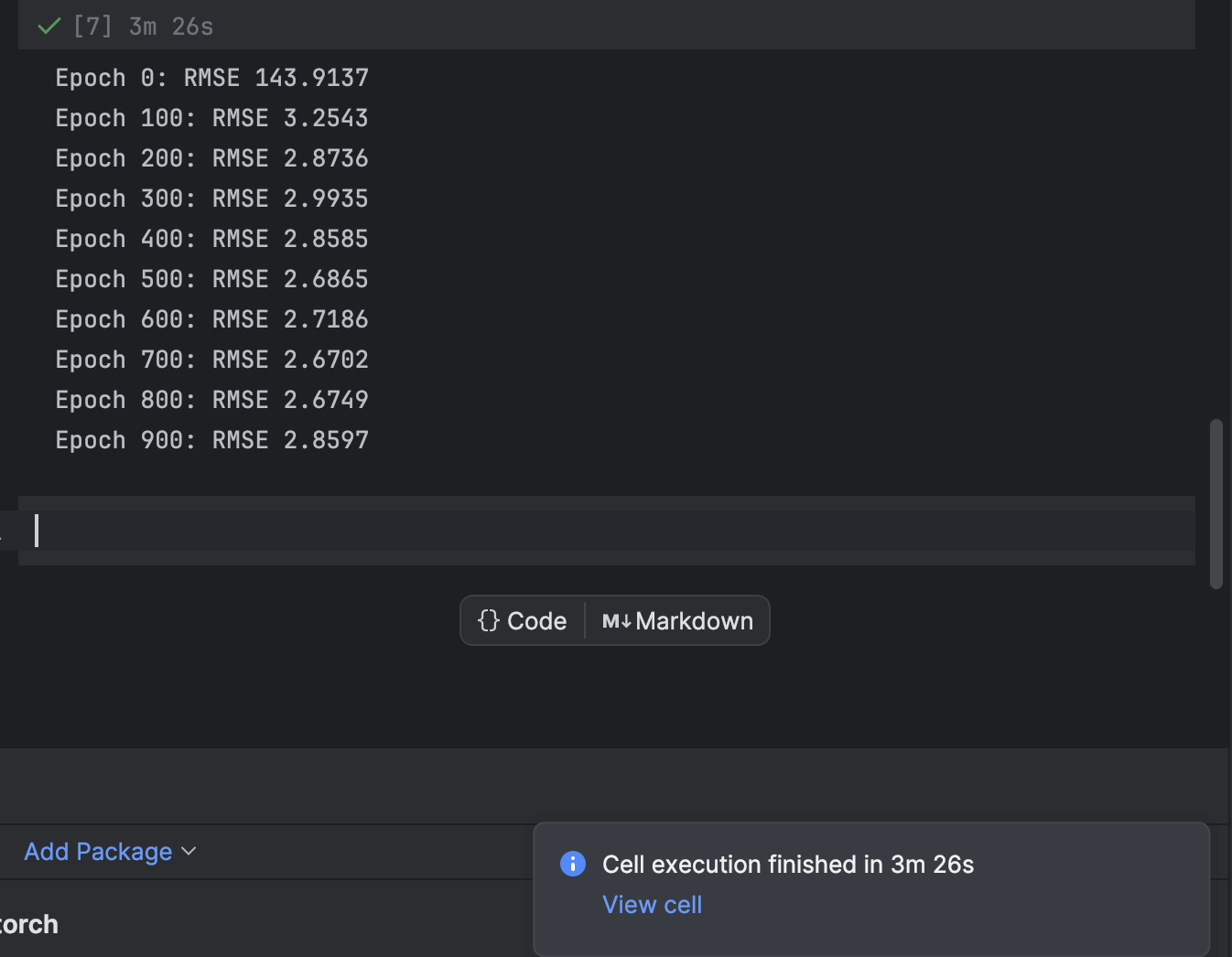
En PyCharm, una celda que requiera cierto tiempo para ejecutarse mostrará una notificación sobre cuánto tiempo queda y un acceso directo a la celda. Esto es muy útil cuando se entrenan modelos de aprendizaje automático, especialmente modelos de aprendizaje profundo, en notebooks de Jupyter.
5. Trazar la predicción y encontrar los errores
A continuación, crearemos la predicción y generaremos los gráficos junto con la serie temporal real. Tenga en cuenta que tendremos que crear una serie 2D np para que coincida con la serie temporal real. La serie temporal real aparecerá en azul, mientras que la serie temporal prevista aparecerá en rojo.
import matplotlib.pyplot as plt
with torch.no_grad():
pred_series = np.ones_like(timeseries) * np.nan
pred_series[lookback:] = model(X)[:, -1, :]
plt.plot(timeseries, c='b')
plt.plot(pred_series, c='r')
plt.show()
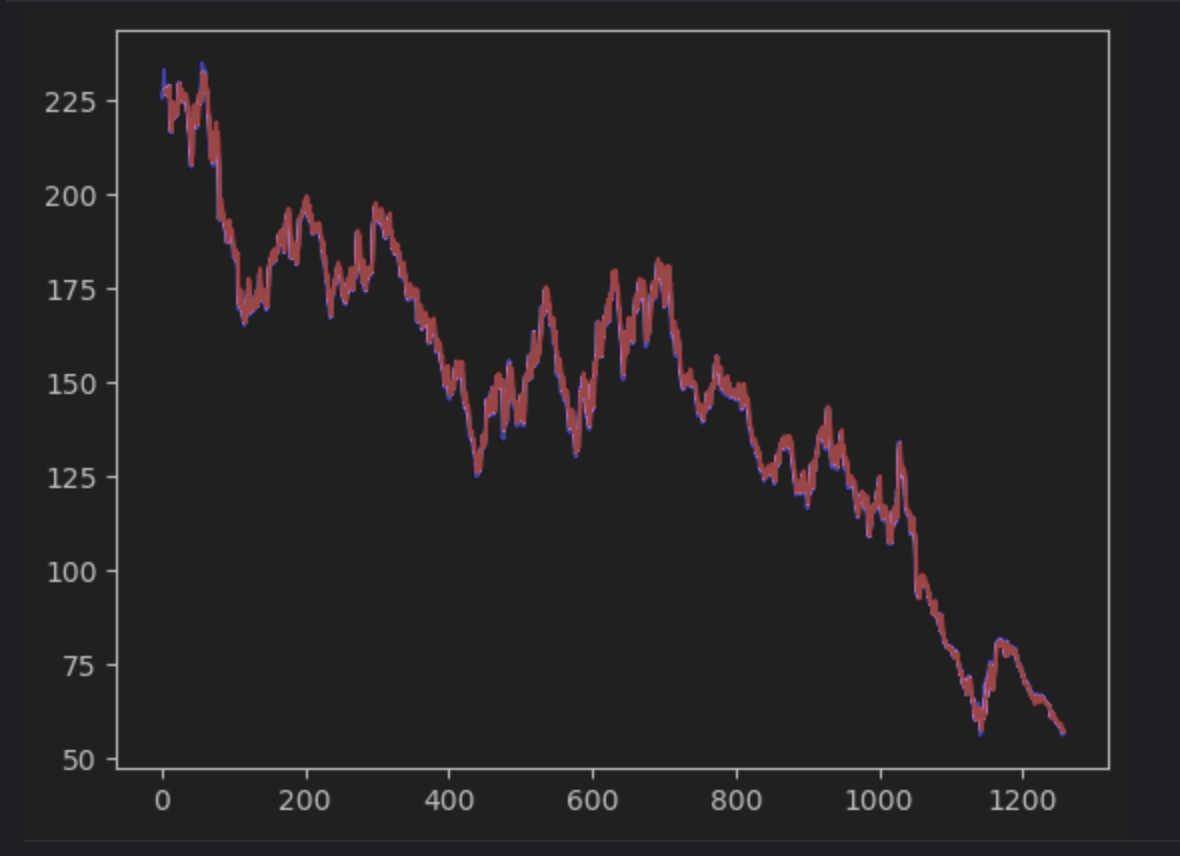
Si observa con atención, verá que la predicción y los valores reales no se alinean perfectamente. Sin embargo, la mayoría de las predicciones funcionan bien.
Para inspeccionar los errores de cerca, podemos crear una serie de errores y utilizar la tabla interactiva para observarlos. Esta vez utilizaremos el error absoluto.
error = abs(timeseries-pred_series) error
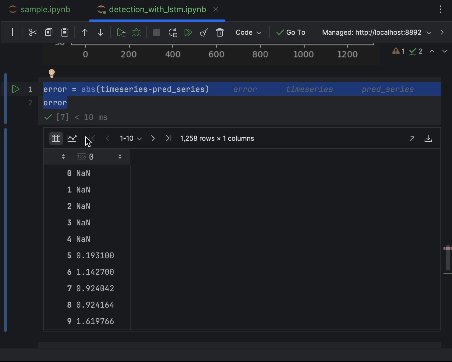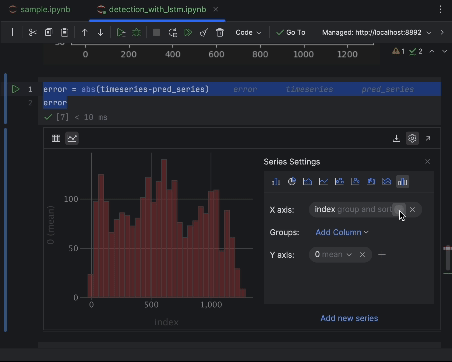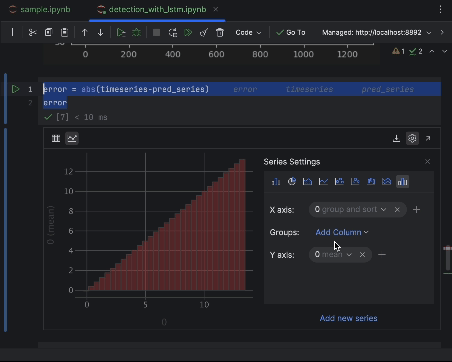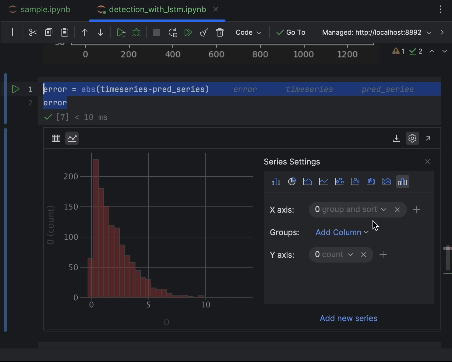
Utilice los ajustes para crear un histograma con el valor del error absoluto como eje x y el recuento del valor como eje y.
6. Decidir el umbral de anomalía y visualizar
La mayoría de los puntos tendrán un error absoluto inferior a 6, por lo que podemos fijarlo como umbral de anomalía. De forma similar a lo que hicimos para las anomalías de la colmena, podemos trazar los puntos de datos anómalos en el gráfico.
threshold = 6
error_series = pd.Series(error.flatten())
price_series = pd.Series(timeseries.flatten())
anomalies_filter = error_series.apply(lambda x: True if x > threshold else False)
anomalies = price_series[anomalies_filter]
plt.figure(figsize=(14, 8))
plt.scatter(x=anomalies.index, y=anomalies, color="red", label="anomalies")
plt.plot(df.index, timeseries, color='blue')
plt.title('Closing price')
plt.xlabel('Days')
plt.ylabel('Price')
plt.legend()
plt.show()
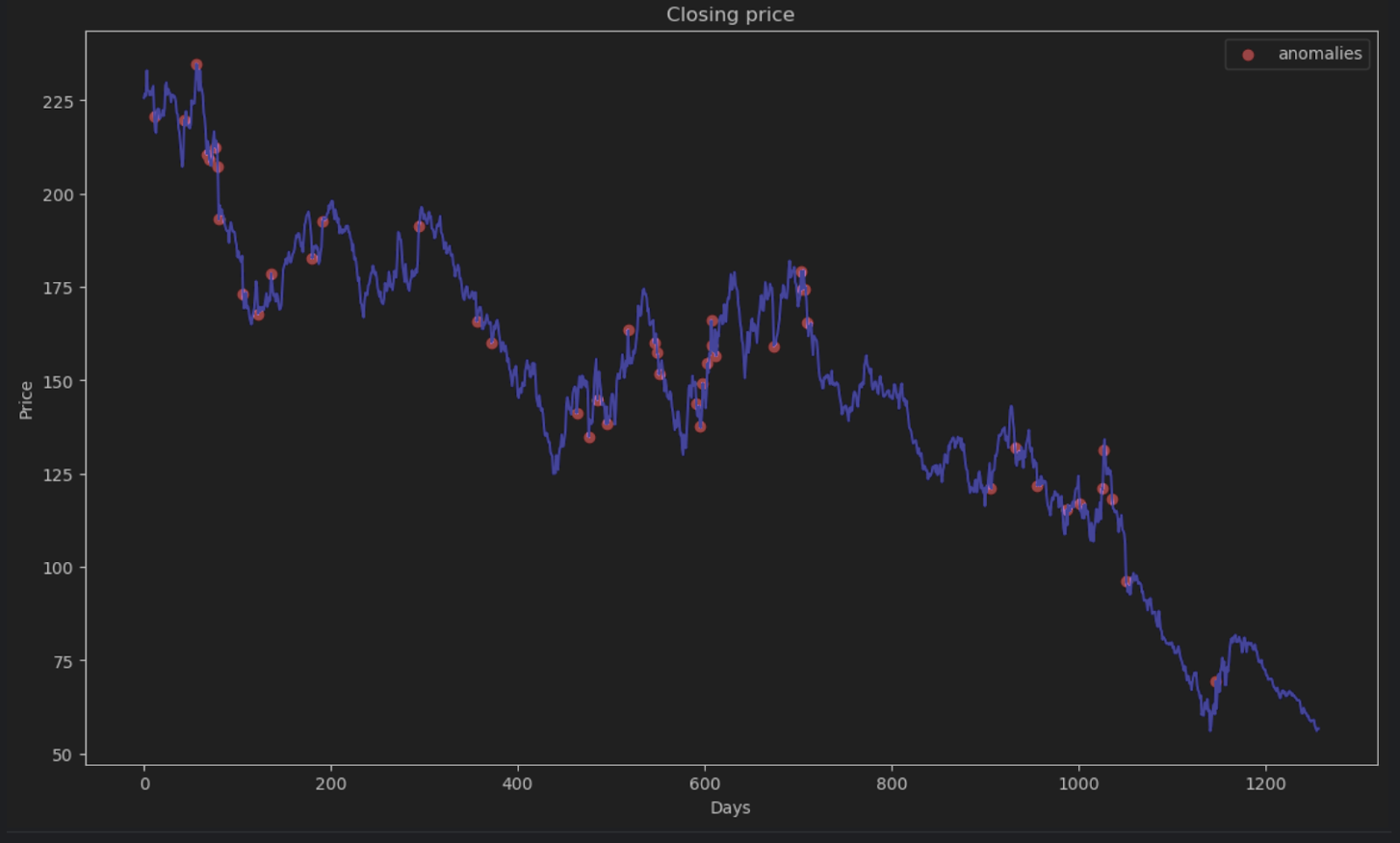
Resumen
Los datos de series temporales son una forma común de datos utilizados en muchas aplicaciones, incluidas las empresariales y la investigación científica. Debido a la naturaleza secuencial de los datos de series temporales, se utilizan métodos y algoritmos especiales para ayudar a determinar anomalías en ellos. En este artículo del blog, demostramos cómo identificar anomalías utilizando la descomposición STL para eliminar estacionalidades y tendencias. También hemos demostrado cómo utilizar el aprendizaje profundo y el modelo LSTM para comparar la estimación prevista y los datos reales con el fin de determinar anomalías.
Detectar anomalías utilizando PyCharm
Con el proyecto Jupyter de PyCharm Professional, puede organizar fácilmente su proyecto de detección de anomalías con muchos archivos de datos y notebooks. Se pueden generar gráficos de salida para inspeccionar las anomalías y los diagramas son muy accesibles en PyCharm. Otras funciones, como las sugerencias de autocompletado, hacen que navegar por todos los modelos de Scikit-learn y los ajustes de trazado de Matplotlib sea una pasada.
Dé un nuevo impulso a sus proyectos de ciencia de datos utilizando PyCharm, y compruebe las funcionalidades de ciencia de datos que ofrece para agilizar su flujo de trabajo de ciencia de datos.
Artículo original en inglés de:
Subscribe to PyCharm Blog updates







