PyCharm
The only Python IDE you need.
Détection des anomalies dans les séries chronologiques

Comment identifier les schémas inhabituels qui peuvent révéler des problèmes critiques ou des opportunités cachées ? La détection des anomalies permet d’identifier les données qui dévient de façon significative par rapport à la norme. Les données de séries chronologiques, qui consistent en données collectées au cours d’une période donnée, reflètent souvent les tendances et les schémas saisonniers. Les anomalies dans les séries chronologiques se produisent lorsque ces schémas sont perturbés, ce qui fait de la détection des anomalies un outil précieux dans des domaines tels que la vente, la finance, la fabrication ou la santé.
Les séries chronologiques présentant des caractéristiques uniques, telles que la saisonnalité et les tendances, des méthodes spécialisées sont requises pour détecter les anomalies efficacement. Dans cet article de blog, nous allons explorer les principales méthodes de détection des anomalies dans les séries chronologiques, avec notamment la décomposition STL et la prédiction LSTM, avec des exemples détaillés de code pour vous aider à commencer.
Détection des anomalies dans les séries chronologiques dans les entreprises
Les données de séries chronologiques sont vitales pour de nombreuses activités et services. La plupart des entreprises appliquent un horodatage aux données enregistrées, afin d’en analyser les changements et de pouvoir les comparer au fil du temps. Les séries chronologiques sont utiles lors de la comparaison d’une certaine quantité pendant une période donnée comme cela est le cas lors d’une comparaison annuelle des données pour mettre en évidence leur caractère saisonnier.
Suivi des ventes
L’un des exemples les plus courants de séries chronologiques saisonnières est les données commerciales. En effet, de nombreuses ventes sont affectées par des congés annuels et la période de l’année, qui constituent des facteurs incontournables d’analyse. Pour cette raison, la décomposition STL représente une méthode très répandue d’analyse et de détection des anomalies, que nous allons couvrir en détail plus bas dans cet article de blog.
Finance
Les données financières, telles que les transactions et les prix des actions, constituent des exemples typiques de données de séries chronologiques. Dans le secteur financier, l’analyse et la détection des anomalies dans ces données constituent une pratique courante. Par exemple, les modèles de prédiction des séries chronologiques peuvent être utilisés lors du trading algorithmique. Nous allons utiliser une prédiction de série temporelle pour identifier les anomalies dans les données boursières plus bas dans cet article de blog.
Fabrication
Un autre cas d’utilisation de la détection des anomalies de séries chronologiques réside dans la détection des défauts sur les lignes de production. Les machines sont également souvent contrôlées, fournissant ainsi des données de séries chronologiques. Il est essentiel de pouvoir avertir la direction en cas de pannes potentielles, et la détection des anomalies joue pour cela un rôle clé.
Médecine et santé
Dans les domaines de la médecine et de la santé, les signes vitaux des patients sont suivis afin de détecter les anomalies. Cela est important pour la recherche médicale et vital pour les diagnostics. Si les signes vitaux d’un patient hospitalisé présentent des anomalies et ne sont pas traités immédiatement, les conséquences peuvent être fatales.
Pourquoi est-il important d’utiliser des méthodes spéciales lors de la détection d’anomalies dans les séries chronologiques ?
Les données de séries chronologiques sont spéciales dans la mesure où elles ne peuvent pas toujours être traitées comme les autres types de données. Par exemple, lorsque nous appliquons une fonction « train test split » (division en ensembles d’entraînement) aux données de séries chronologiques, la nature séquentielle des données signifie que nous ne pouvons pas en changer l’ordre. Cela se vérifie également lors de l’application de données de séries chronologiques à un modèle de deep learning. Un réseau neuronal récurrent (RNN) est généralement utilisé pour prendre la relation séquentielle en compte, et les données d’entraînement sont entrées sous forme de fenêtres temporelles, ce qui préserve la séquence des événements qu’elles contiennent.
Les données de séries chronologiques sont également spéciales dans la mesure où elles sont soumises à des facteurs saisonniers et des tendances que nous ne pouvons pas ignorer. Ce caractère saisonnier peut prendre la forme d’un cycle de 24 heures, de 7 jours ou de 12 mois, pour ne citer que les cas les plus courants. Les anomalies ne peuvent être déterminées qu’une fois les facteurs saisonniers et les tendances pris en compte, comme vous pourrez le voir dans notre exemple ci-dessous.
Méthodes utilisées pour la détection des anomalies dans les séries chronologiques
Dans la mesure où les données de séries chronologiques sont spéciales, des méthodes spécifiques sont nécessaires pour y détecter des anomalies. Selon le type de données, une partie des méthodes et des algorithmes que nous avons mentionnés dans le précédent article sur la détection des anomalies peut être utilisée sur les données de séries chronologiques. Toutefois, avec ces méthodes, la détection des anomalies peut ne pas être aussi robuste qu’avec celles qui ont été conçues spécifiquement pour les données de séries chronologiques. Dans certains cas, une combinaison de méthodes de détection peut être utilisée pour confirmer à nouveau le résultat de la détection et éviter les faux positifs ou négatifs.
Décomposition STL
L’une des solutions les plus populaires d’utilisation des données de séries chronologiques saisonnières est la décomposition STL, la décomposition de tendance saisonnière appliquant la régression locale ou LOESS (locally estimated scatterplot smoothing). Dans cette méthode, une série chronologique est décomposée en utilisant une estimation de la saisonnalité (la période étant fournie ou déterminée par un algorithme), une tendance (estimée) et la composante résiduelle (le bruit dans les données). Statsmodels est l’une des bibliothèques Python qui fournit des outils de décomposition STL.
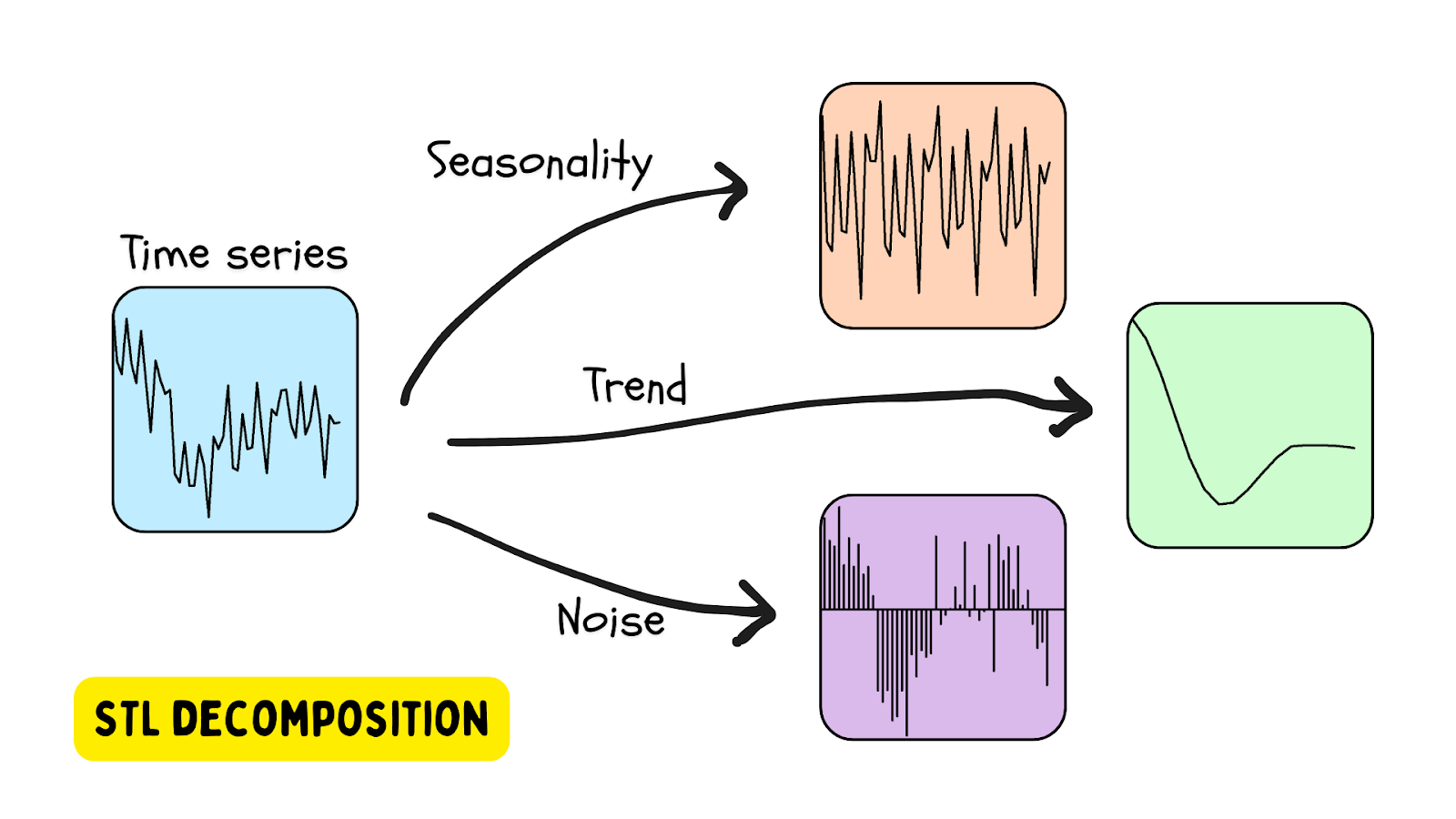
Une anomalie est détectée lorsque le résidu dépasse un certain seuil.
Application de la décomposition STL aux données d’une ruche
Dans un article de blog précédent, nous avons parlé de la détection des anomalies dans les ruches au moyen des méthodes OneClassSVM et IsolationForest.
Dans ce tutoriel, nous allons analyser les données d’une ruche en tant que série chronologique avec la classe STL fournie par la bibliothèque statsmodels. Pour commencer, configurez votre environnement en utilisant le fichier suivant : requirements.txt.
1. Installer la bibliothèque
Dans la mesure où nous avons uniquement utilisé le modèle fourni par Scikit-learn, nous devons installer la bibliothèque statsmodels fournie par PyPI. Cela est simple à faire dans PyCharm.
Ouvrez la fenêtre Python Packages (choisissez l’icône en bas à gauche de l’IDE) et tapez statsmodels dans la zone de recherche.
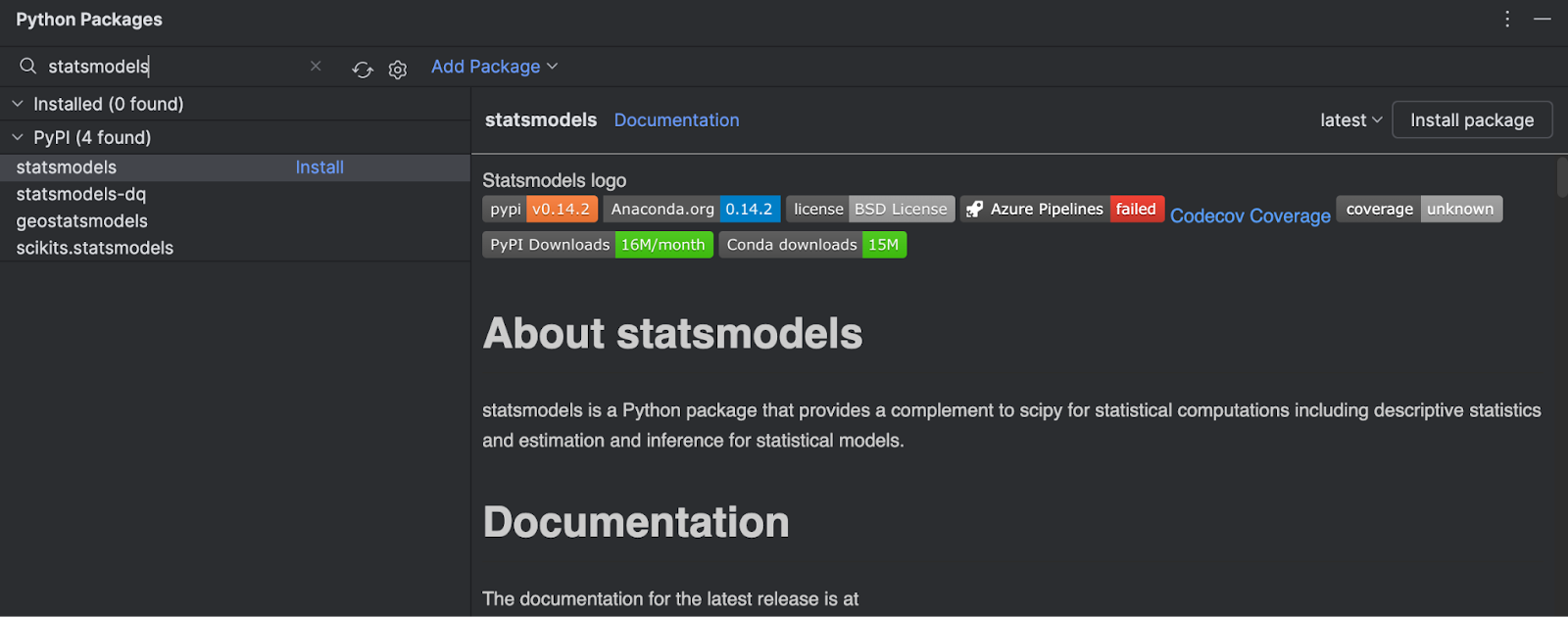
Vous trouverez toutes les informations sur le paquet dans la partie droite. Pour l’installer, cliquez simplement sur Install package.
2. Créer un notebook Jupyter
Pour analyser plus en détail l’ensemble de données, nous allons créer un notebook Jupyter pour profiter des outils fournis par l’environnement de notebook Jupyter de PyCharm.
Nous allons importer pandas et charger le fichier .csv.
import pandas as pd
df = pd.read_csv('../data/Hive17.csv', sep=";")
df = df.dropna()
df
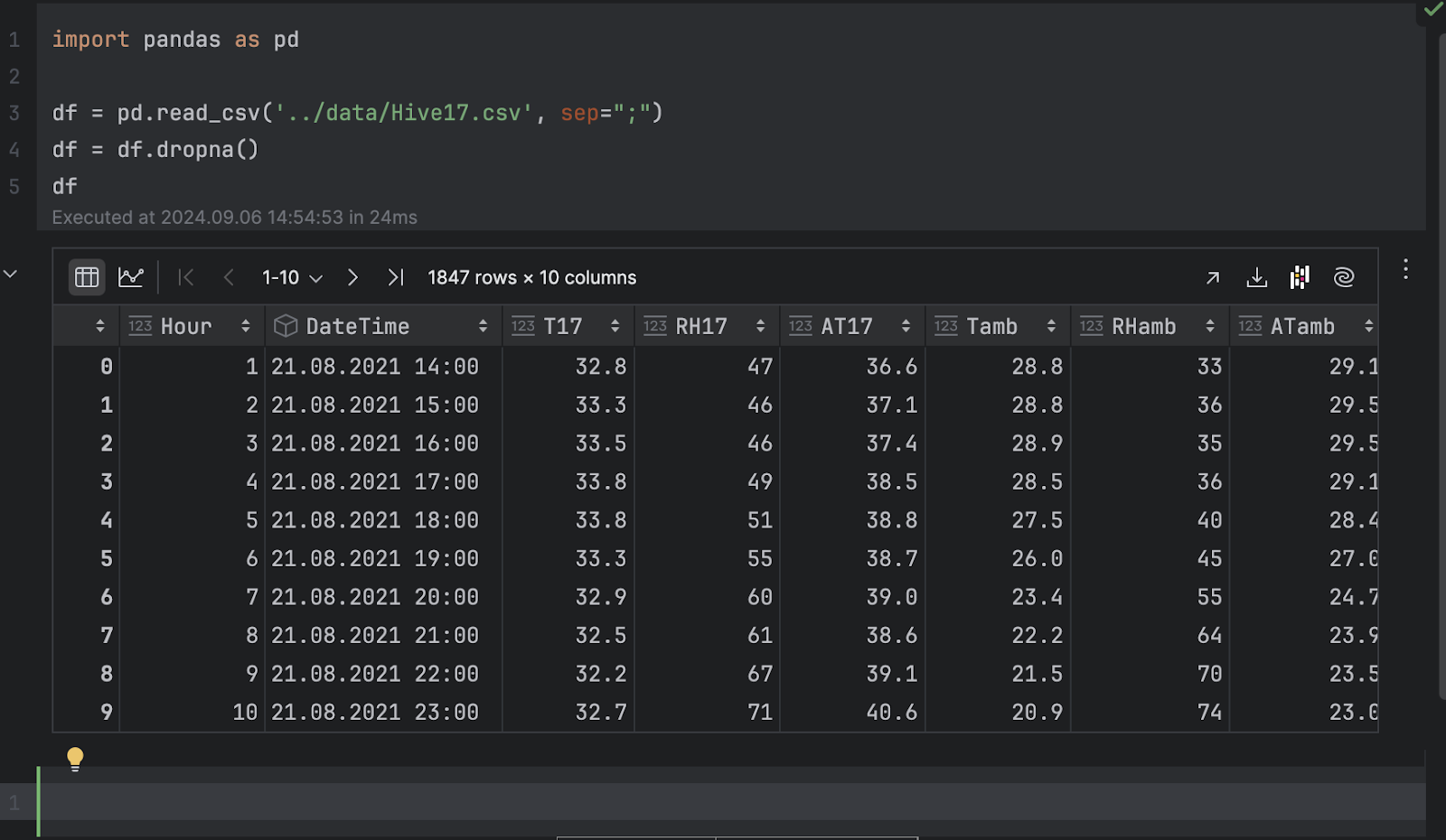
3. Inspecter les données sous forme de graphiques
Nous allons maintenant inspecter les données sous forme de graphiques. Dans cet exemple, nous voulons voir l’évolution de la température de la ruche 17. Cliquez sur Chart view dans l’inspecteur de dataframe, puis choisissez T17 en tant qu’axe y dans les paramètres de série.
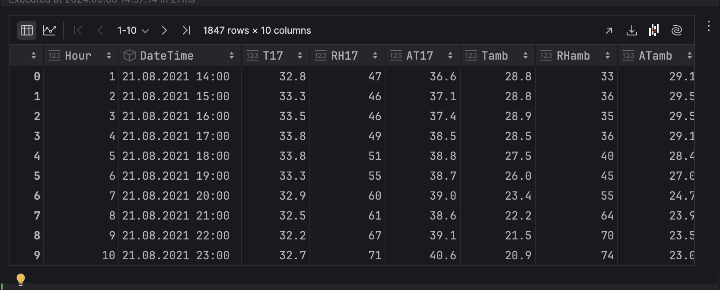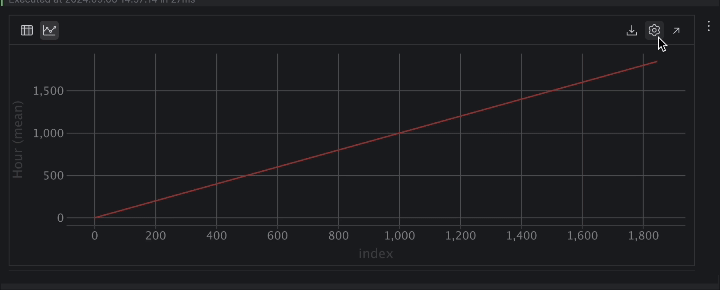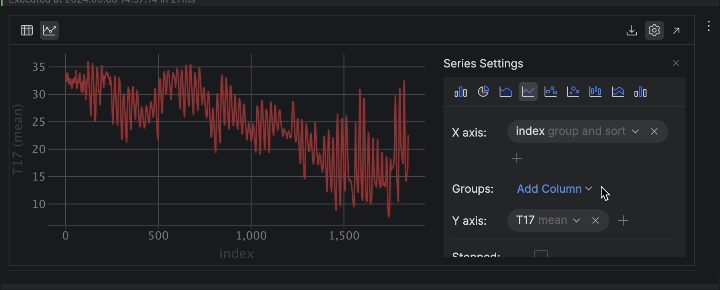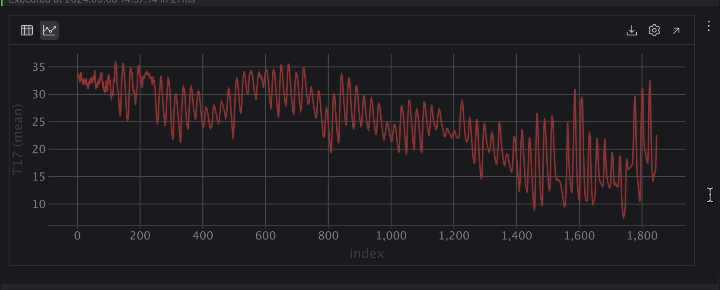
Lorsqu’elle est exprimée sous forme chronologique, la température présente de nombreuses variations. Cela indique un comportement périodique, probablement dû au cycle jours/nuits, ce qui permet d’affirmer qu’il s’agit de mesures de température sur une période de 24 heures.
Ensuite, il y a une tendance de baisse des températures dans le temps. Si vous examinez la colonne DateTime, vous pouvez voir la plage de dates d’août à novembre. Dans la mesure où la page Kaggle de l’ensemble de données indique que les données ont été collectées en Turquie, la transition de l’été à l’automne explique la baisse observée des températures dans le temps.
4. Décomposition de la série chronologique
Pour comprendre la série chronologique et détecter les anomalies, nous allons effectuer une décomposition STL, en important la classe STL depuis statsmodels et en l’adaptant à nos données de température.
from statsmodels.tsa.seasonal import STL stl = STL(df["T17"], period=24, robust=True) result = stl.fit()
Nous devons fournir une période pour réaliser la décomposition. Comme nous l’avons mentionné plus tôt, il s’agit bien d’un cycle de 24 heures.
Selon la documentation, STL décompose une série chronologique en trois composants : tendance, saisonnalité et résidu. Pour avoir une vue plus claire du résultat décomposé, nous pouvons utiliser la méthode plot :
result.plot()
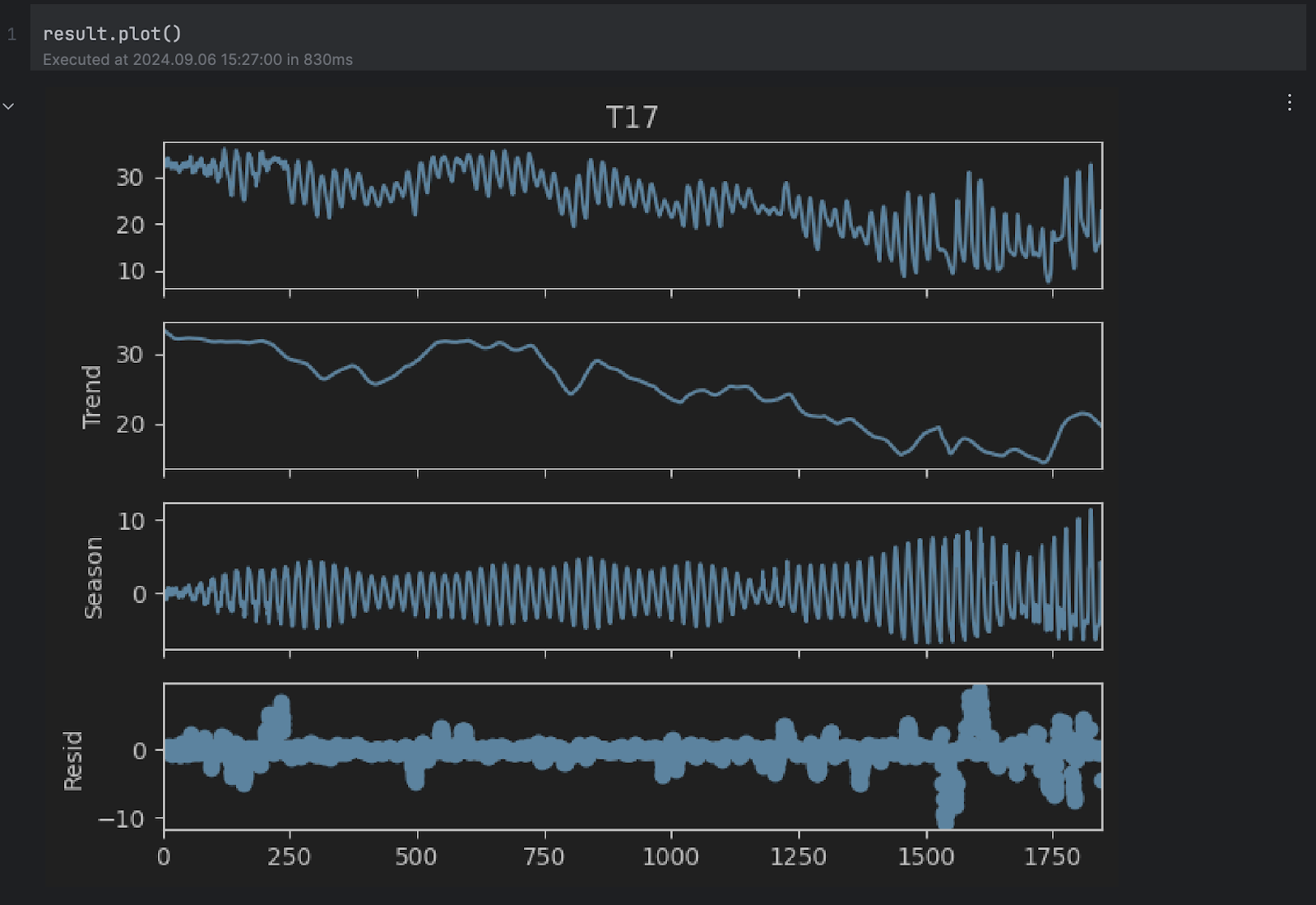
Vous pouvez voir que les graphiques Trend et Season semblent corroborer nos hypothèses ci-dessus. Toutefois, nous sommes intéressés par la courbe résiduelle en bas, qui représente la série d’origine sans les changements propres à la tendance et la saisonnalité. Toute valeur extrêmement haute ou basse dans la composante résiduelle dénote une anomalie.
5. Seuil d’anomalie
Ensuite, nous devons déterminer quelles valeurs de la composante résiduelle doivent être considérées comme anormales. Pour cela, nous allons examiner l’histogramme de la composante résiduelle.
result.resid.plot.hist()
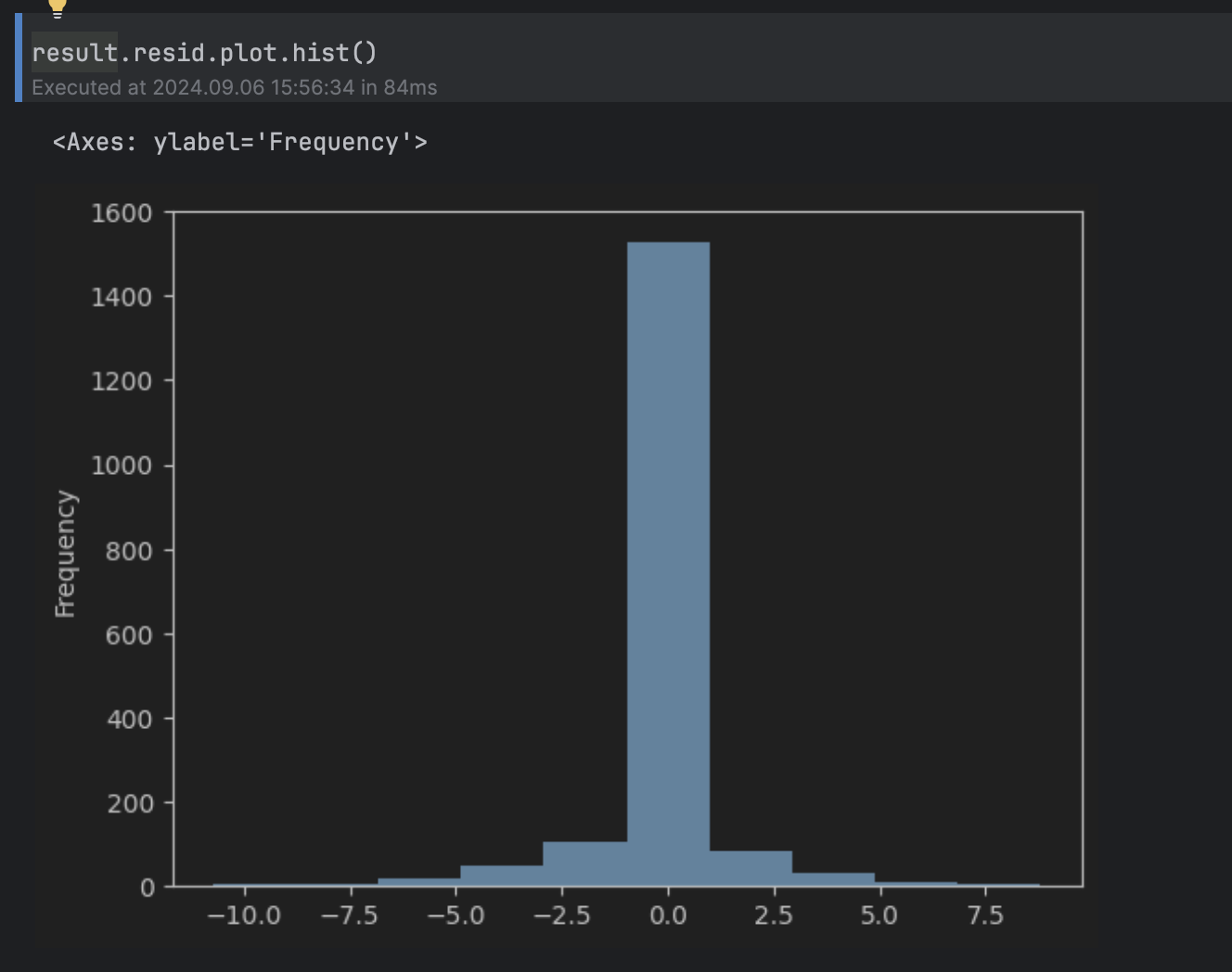
Cela peut être considéré comme une distribution normale autour de 0, avec une queue longue au-dessus de 5 et en dessous de -5, ce qui nous amène à définir le seuil sur 5.
Pour afficher les anomalies des séries chronologiques d’origine, nous pouvons les colorer toutes en rouge dans le graphique, de la façon suivante :
import matplotlib.pyplot as plt
threshold = 5
anomalies_filter = result.resid.apply(lambda x: True if abs(x) > threshold else False)
anomalies = df["T17"][anomalies_filter]
plt.figure(figsize=(14, 8))
plt.scatter(x=anomalies.index, y=anomalies, color="red", label="anomalies")
plt.plot(df.index, df['T17'], color='blue')
plt.title('Temperatures in Hive 17')
plt.xlabel('Hours')
plt.ylabel('Temperature')
plt.legend()
plt.show()
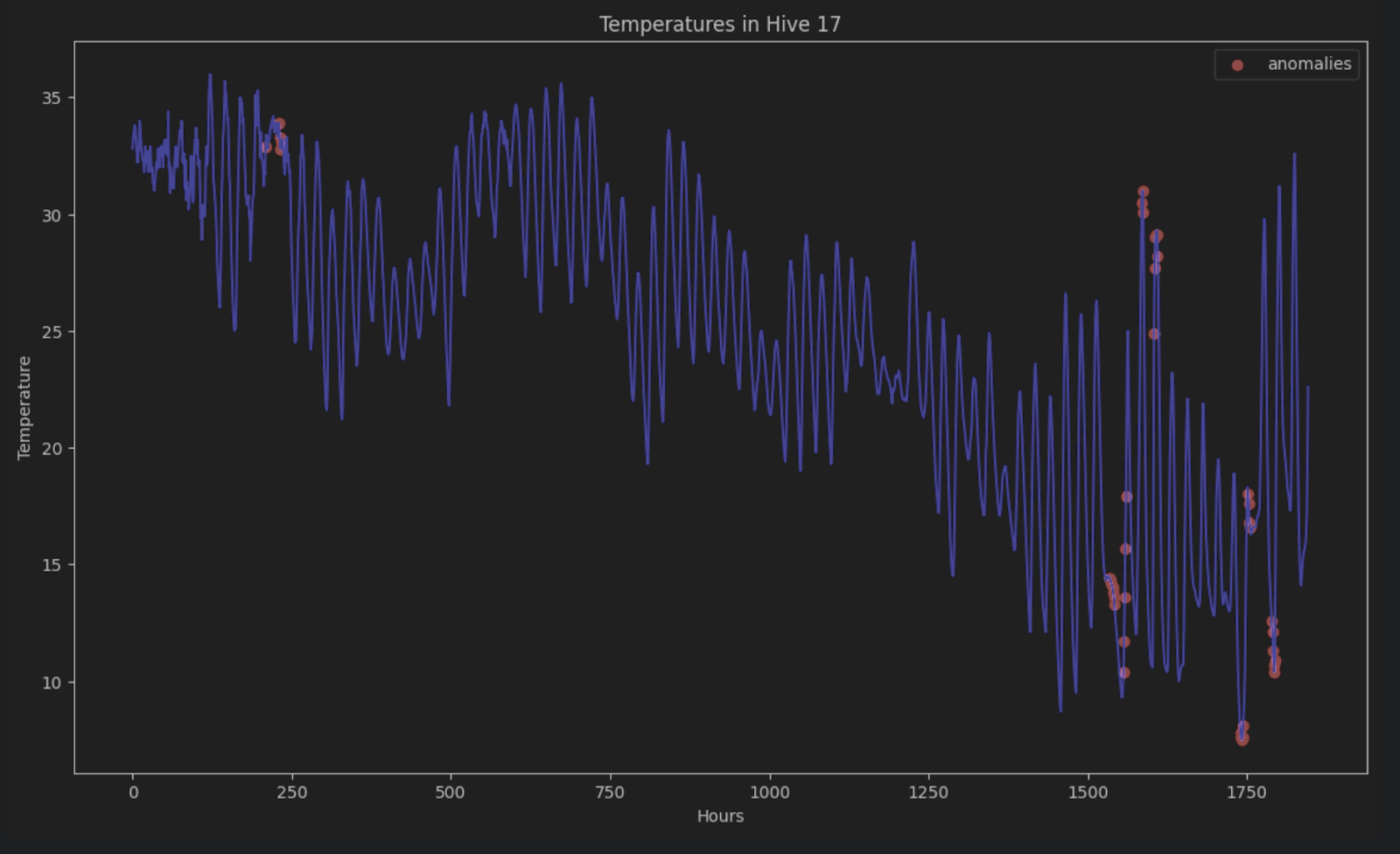
En l’absence de décomposition STL, il est très difficile d’identifier ces anomalies dans une série chronologique comprenant des périodes et des tendances.
Prévision LSTM
Une autre possibilité de détection des anomalies dans les séries chronologiques consiste à faire des prévisions sur ces séries en appliquant des méthodes de deep learning pour estimer le résultat des points de données. Si une estimation est très différente du point de données réel, cela peut être le signe de données anormales.
L’un des algorithmes de deep learning les plus populaires pour prédire les données séquentielles est le modèle LSTM (Long short-term memory – mémoire long-court terme), qui est un type de réseau neuronal récurrent (RNN). Le modèle LSTM a des portes d’entrée, d’oubli et de sortie, qui sont des matrices de nombres. Cela permet de transférer des informations importantes lors de l’itération suivante des données.
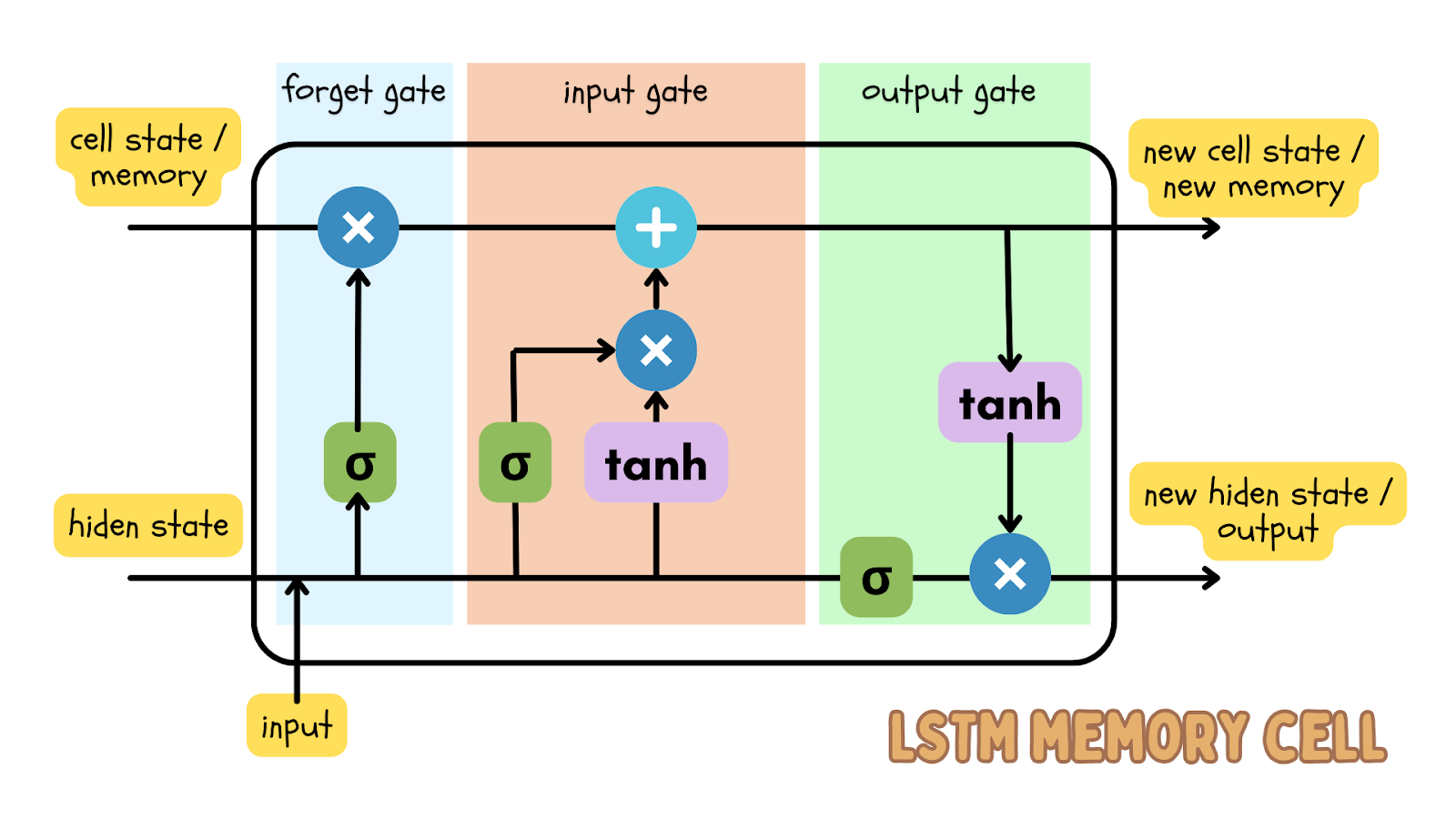
Les séries chronologiques sont des données séquentielles, ce qui veut dire que l’ordre des points de données ne doit pas être modifié. Par conséquent, le modèle LSTM est un modèle efficace de deep learning pour prédire le résultat à un moment donné. Cette prévision peut ensuite être comparée aux données réelles et il est possible de définir un seuil pour déterminer si les données réelles constituent une anomalie.
Application des prévisions LSTM aux cotations en bourse
Nous allons créer un projet Jupyter pour détecter les anomalies de cotation des actions Apple au cours des 5 dernières années. L’ensemble de données sur le prix des actions offre les données les plus récentes. Si vous souhaitez essayer cet exemple tout en lisant l’article, vous pouvez télécharger l’ensemble de données que nous utilisons.
1. Créer un projet Jupyter
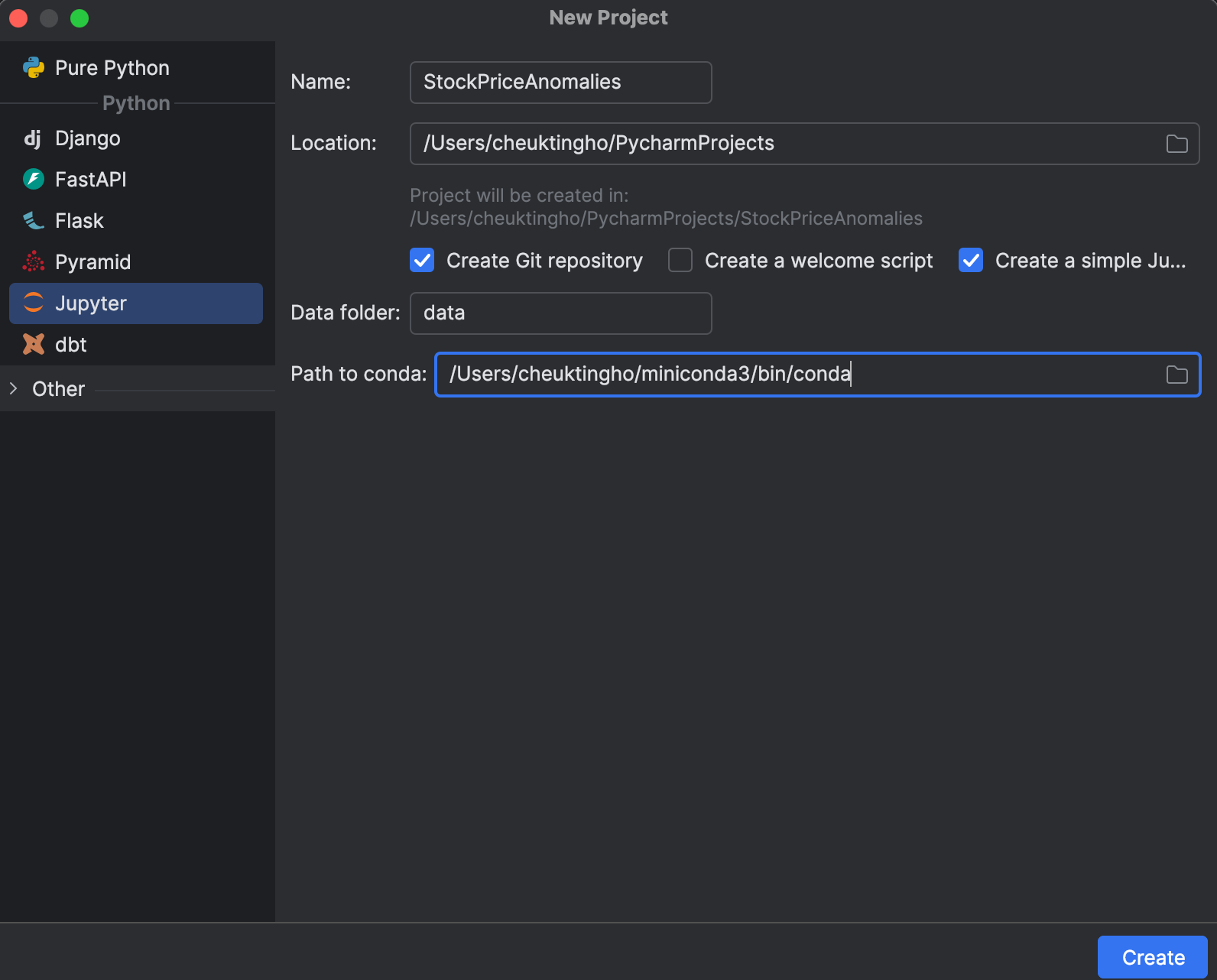
Lors de la création d’un projet, vous pouvez opter pour une version Jupyter, car elle est optimisée pour la science des données. Dans la fenêtre New Project, vous pouvez créer un référentiel Git et déterminer quelle installation conda utiliser pour gérer votre environnement.
Une fois le projet créé, un exemple de notebook s’affiche. Vous pouvez alors créer un notebook Jupyter pour cet exercice.
Ensuite, nous allons configurer requirements.txt. Nous aurons besoin de pandas, matplotlib et PyTorch, qui est appelé torch dans PyPI. Dans la mesure où PyTorch n’est pas inclus dans l’environnement conda, PyCharm nous indique que ce paquet est manquant. Pour l’installer, cliquez sur l’icône d’ampoule et sélectionnez Install all missing packages.
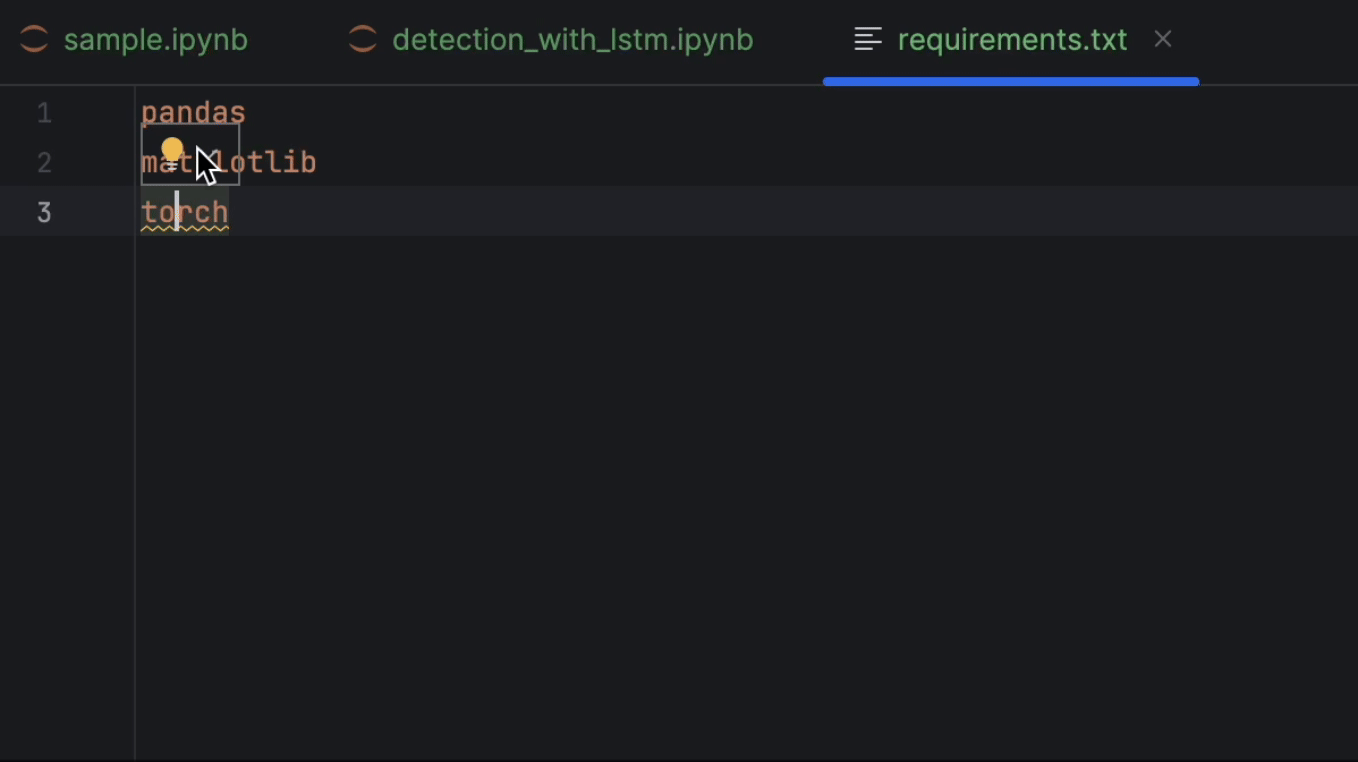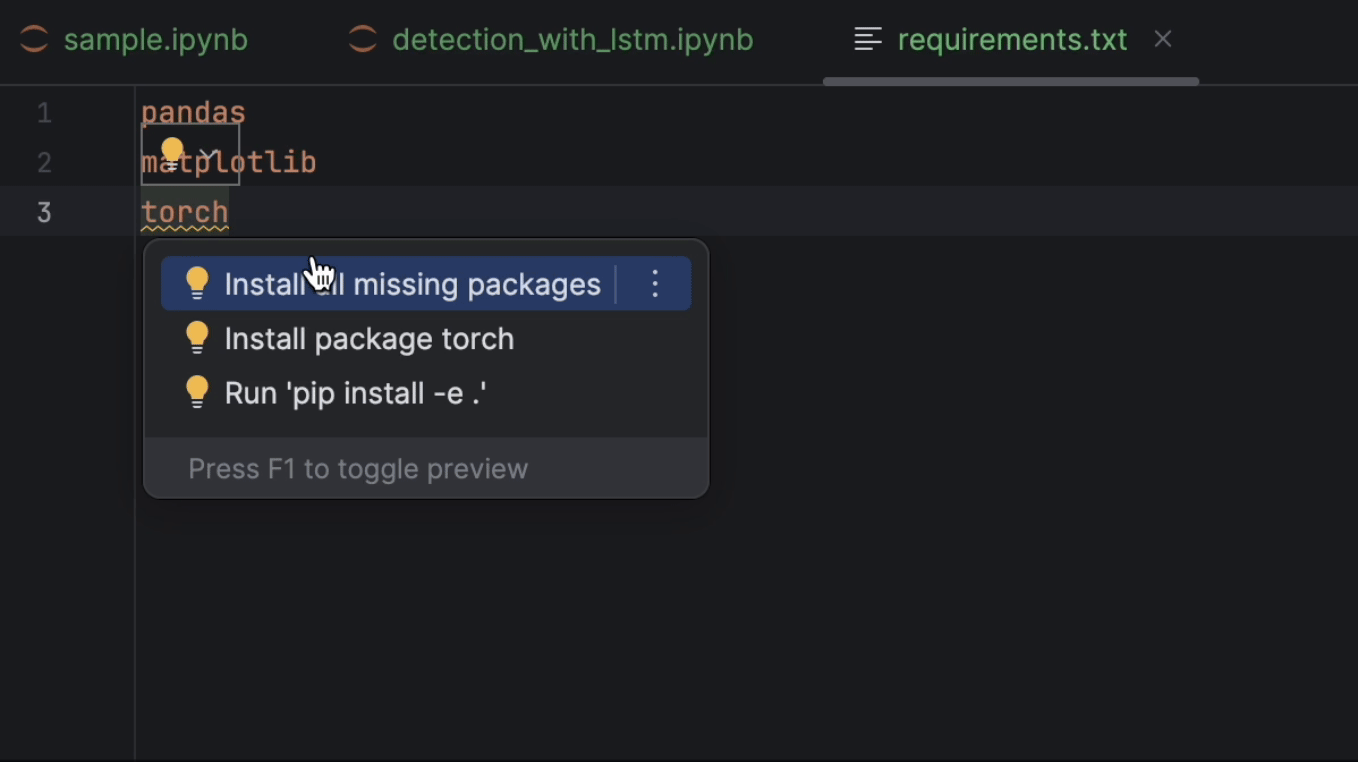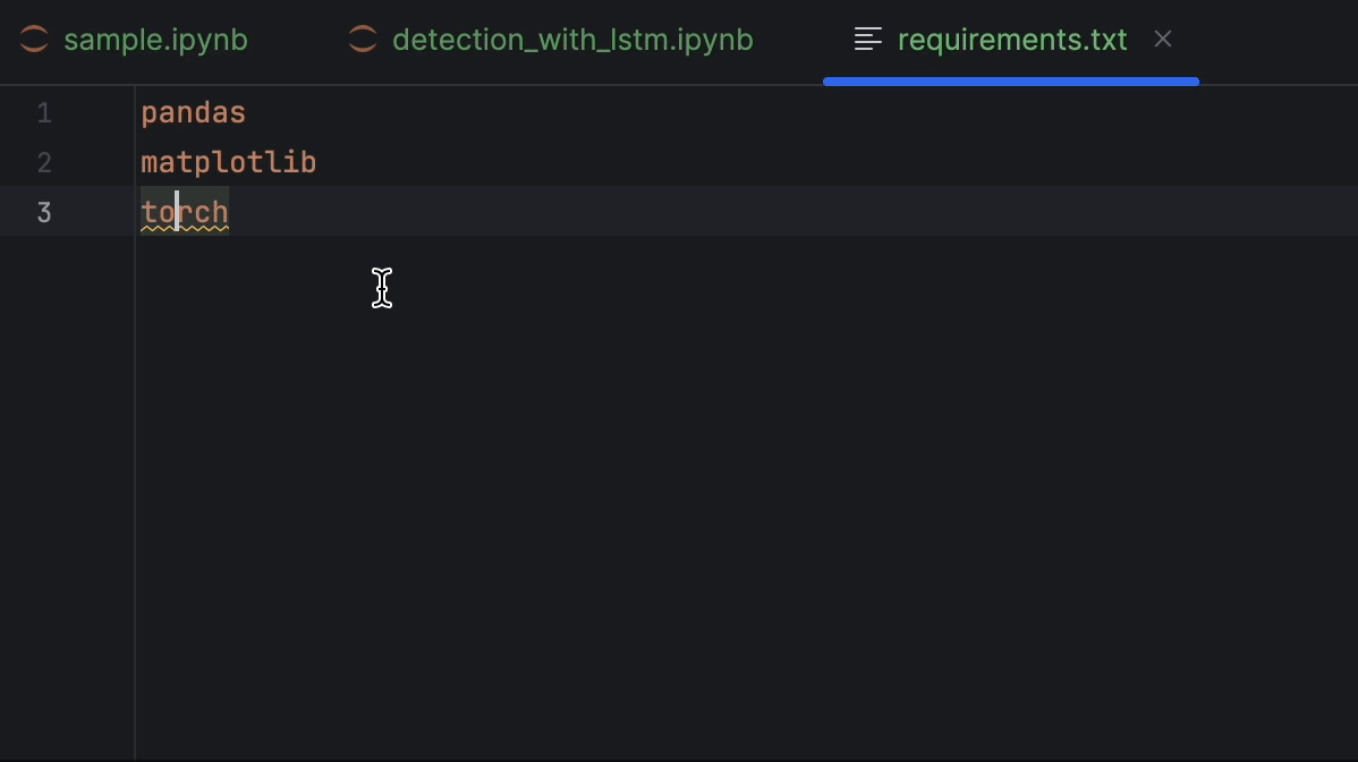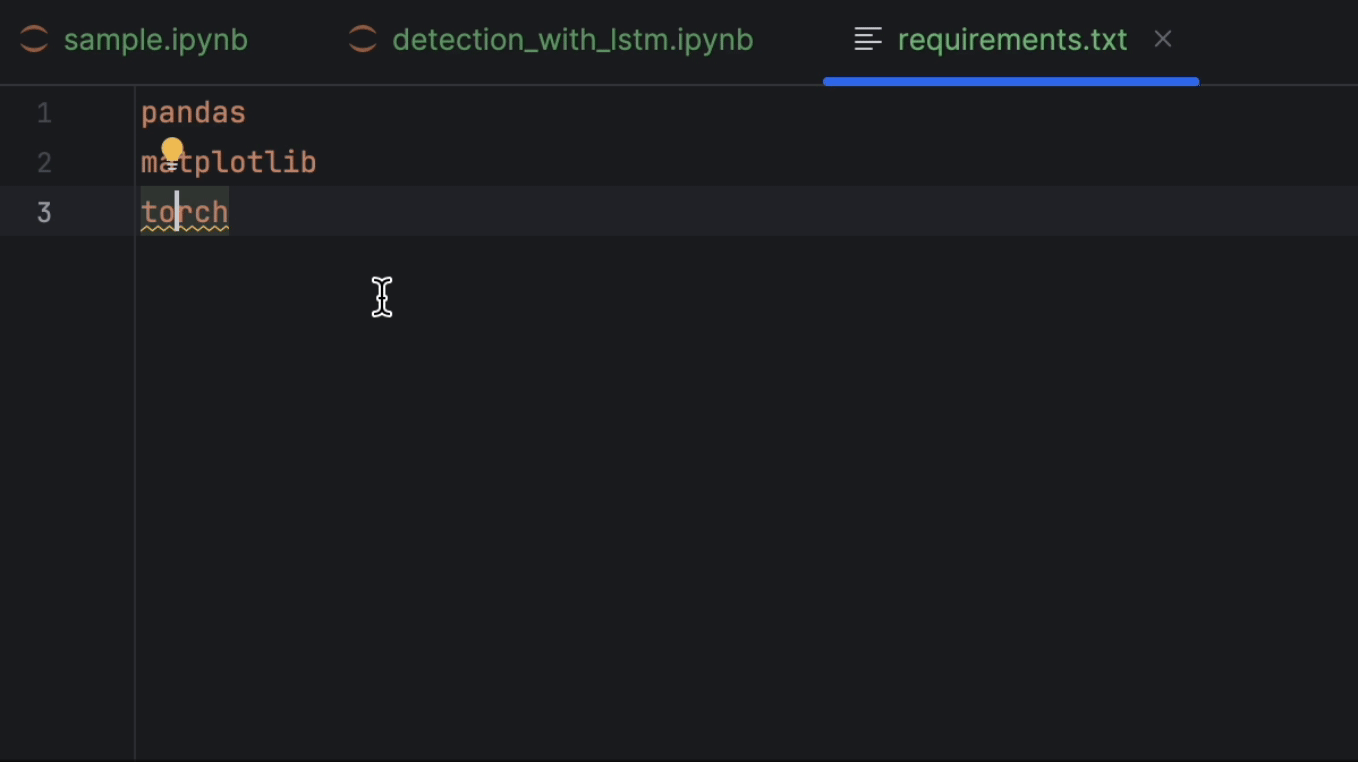
2. Chargement et inspection des données
Ensuite, nous allons placer notre ensemble de données apple_stock_5y.csv dans le dossier de données et le charger en tant que DataFrame pandas pour l’inspecter.
import pandas as pd
df = pd.read_csv('data/apple_stock_5y.csv')
df
La table interactive permet de déterminer facilement si des données sont manquantes.
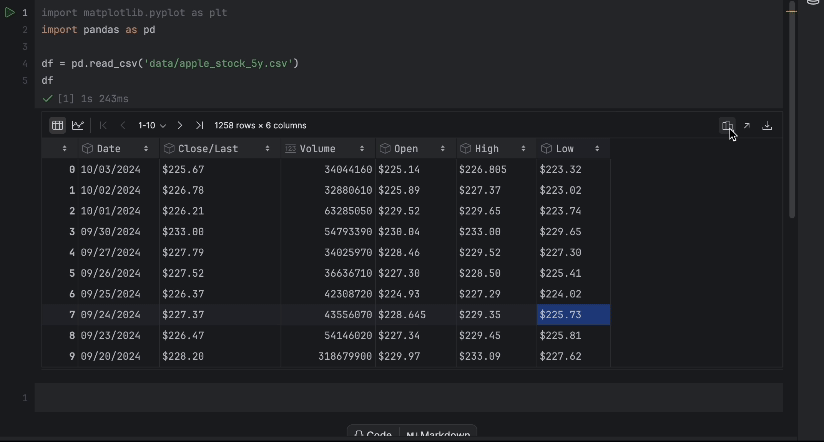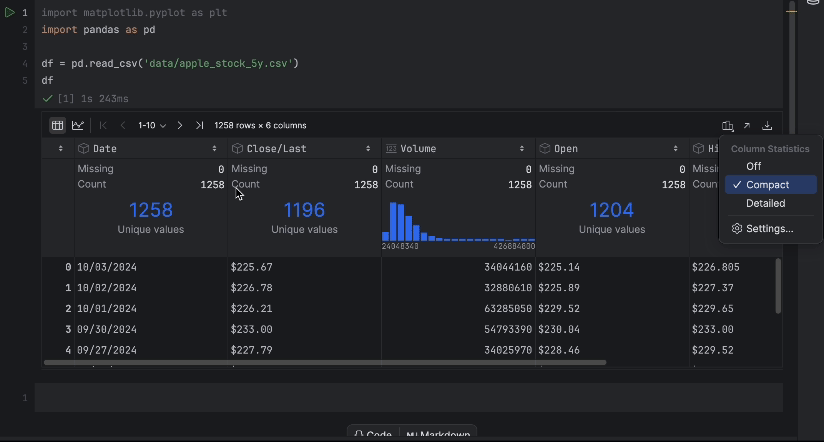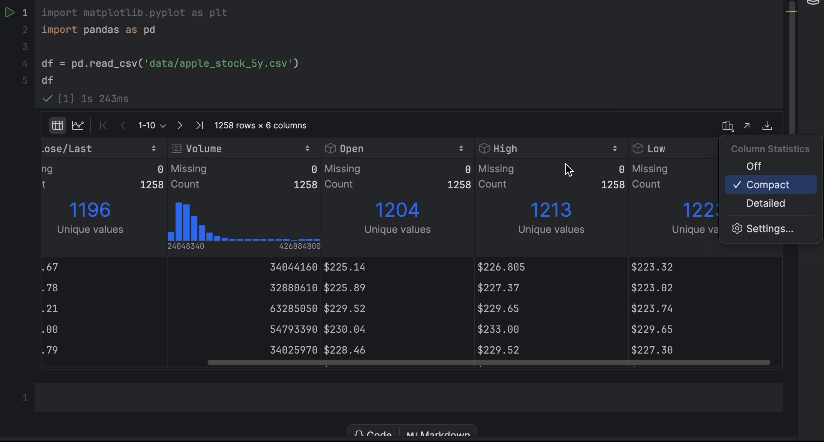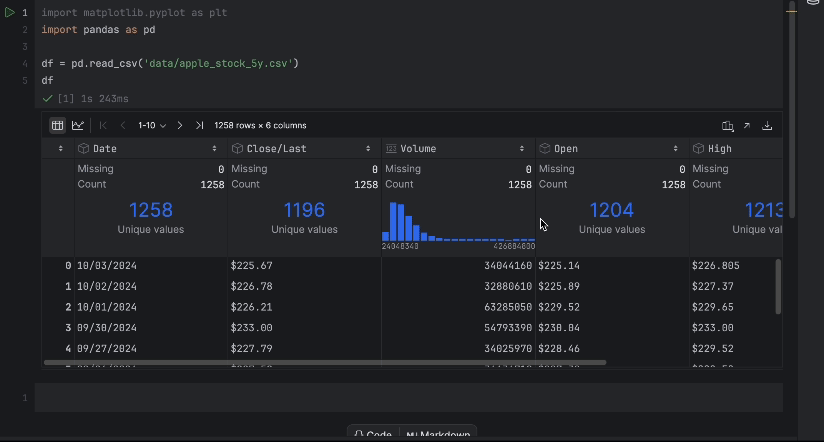
Il n’y a pas de données manquantes, mais nous avons un problème, nous voulons utiliser le prix Close/Last, mais il ne s’agit pas d’un type de données numérique. Nous allons opérer une conversion et inspecter nos données à nouveau :
df["Close/Last"] = df["Close/Last"].apply(lambda x: float(x[1:])) df
À présent, nous pouvons inspecter le prix avec le tableau interactif. Cliquez sur l’icône de traçage à gauche pour créer un tracé. Par défaut, il utilise Date comme axe des x et Volume comme axe des y. Dans la mesure où nous devons inspecter le prix Close/Last, allez dans la section des paramètres en cliquant sur l’icône d’engrenage à droite et choisissez Close/Last comme axe des y.
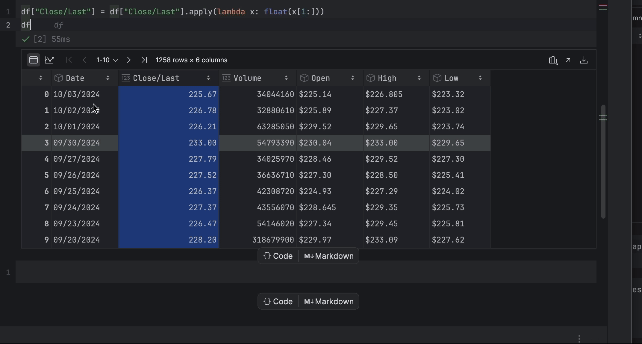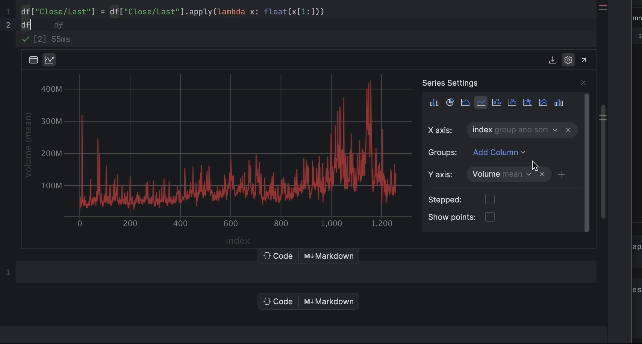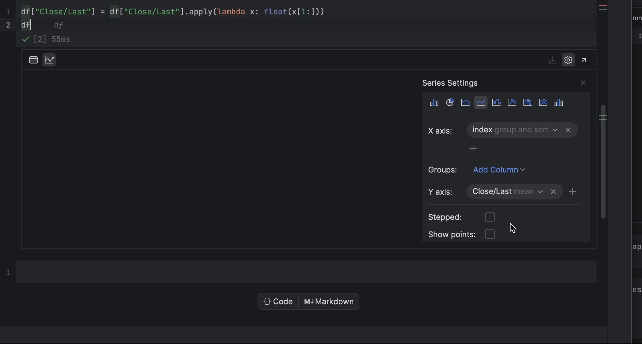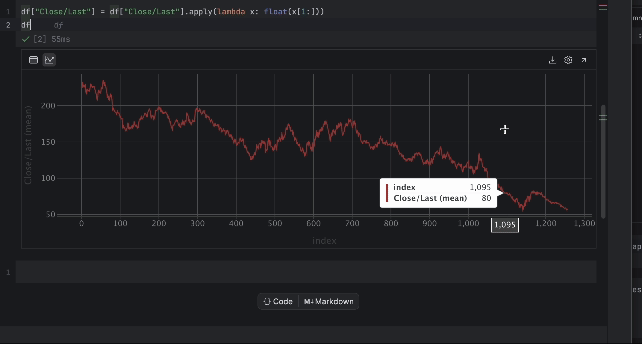
3. Préparation des données d’entraînement pour LSTM
Ensuite, nous devons préparer les données d’entraînement à utiliser dans le modèle LSTM. Nous devons préparer une séquence de vecteurs (feature X), chacun représentant une fenêtre de temps, pour prédire le prix suivant. Le prix suivant formera une autre séquence (target y). Ici, nous pouvons définir la taille de cette fenêtre de temps avec la variable lookback. Le code suivant crée les séquences X et y qui seront converties en tenseurs PyTorch :
import torch
lookback = 5
timeseries = df[["Close/Last"]].values.astype('float32')
X, y = [], []
for i in range(len(timeseries)-lookback):
feature = timeseries[i:i+lookback]
target = timeseries[i+1:i+lookback+1]
X.append(feature)
y.append(target)
X = torch.tensor(X)
y = torch.tensor(y)
print(X.shape, y.shape)
De manière générale, plus la fenêtre est large, plus notre modèle sera grand, car le vecteur d’entrée est plus grand. Toutefois, avec une plus grande fenêtre, la séquence d’entrées sera plus courte. Par conséquent, la définition de cette fenêtre d’antécédent est une question d’équilibre. Nous allons commencer par 5, mais n’hésitez pas à essayer d’autres valeurs pour voir la différence.
4. Création et entraînement du modèle
Nous allons créer le modèle en utilisant une classe avec le module nn de PyTorch avant de l’entraîner. Le module nn fournit les différentes briques, qui correspondent aux différentes couches d’un réseau neuronal. Dans cet exercice, nous allons créer une couche LSTM simple, suivie par une couche linéaire:
import torch.nn as nn
class StockModel(nn.Module):
def __init__(self):
super().__init__()
self.lstm = nn.LSTM(input_size=1, hidden_size=50, num_layers=1, batch_first=True)
self.linear = nn.Linear(50, 1)
def forward(self, x):
x, _ = self.lstm(x)
x = self.linear(x)
return x
Ensuite, nous allons entraîner notre modèle. Avant cela, nous devons créer un optimiseur, une fonction de perte permettant de calculer la perte entre les valeurs y prévues et réelles, et un chargeur de données pour entrer nos données d’entraînement :
import numpy as np import torch.optim as optim import torch.utils.data as data model = StockModel() optimizer = optim.Adam(model.parameters()) loss_fn = nn.MSELoss() loader = data.DataLoader(data.TensorDataset(X, y), shuffle=True, batch_size=8)
Le chargeur de données peut changer l’ordre des entrées, car nous avons déjà créé les fenêtres de temps. Cela permet de préserver la relation séquentielle dans chaque fenêtre.
L’entraînement se fait en utilisant une boucle for pour chaque époque. Toutes les 100 époques, nous imprimons la perte et observons la convergence du modèle :
n_epochs = 1000
for epoch in range(n_epochs):
model.train()
for X_batch, y_batch in loader:
y_pred = model(X_batch)
loss = loss_fn(y_pred, y_batch)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 != 0:
continue
model.eval()
with torch.no_grad():
y_pred = model(X)
rmse = np.sqrt(loss_fn(y_pred, y))
print(f"Epoch {epoch}: RMSE {rmse:.4f}")
Nous commençons à 1 000 époques, mais le modèle converge très rapidement. N’hésitez pas à essayer un autre nombre d’époques lors de l’entraînement pour obtenir le meilleur résultat possible.
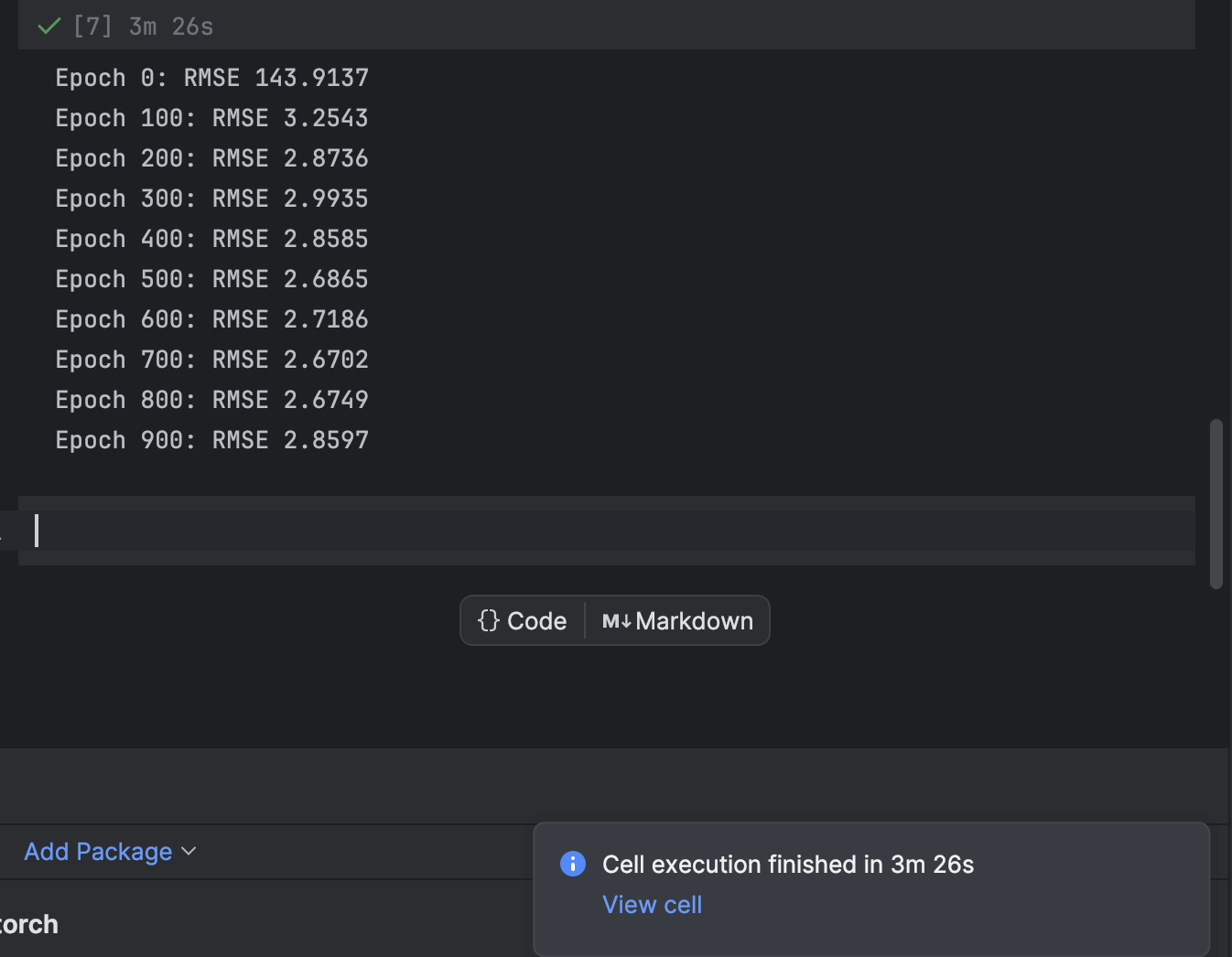
Dans PyCharm, une cellule qui demande un temps d’exécution donne une indication du temps restant et un raccourci vers la cellule. Cela est particulièrement pratique lors de l’entraînement des modèles de machine learning, notamment pour le deep learning, dans les notebooks Jupyter.
5. Tracer la prévision et trouver les erreurs
Ensuite, nous allons créer la prévision et la tracer en utilisant les séries chronologiques réelles. Nous allons cependant devoir créer une série np 2D qui devra correspondre avec la série chronologique réelle. La série chronologique réelle sera en bleu, tandis que la série prédite sera en rouge.
import matplotlib.pyplot as plt
with torch.no_grad():
pred_series = np.ones_like(timeseries) * np.nan
pred_series[lookback:] = model(X)[:, -1, :]
plt.plot(timeseries, c='b')
plt.plot(pred_series, c='r')
plt.show()
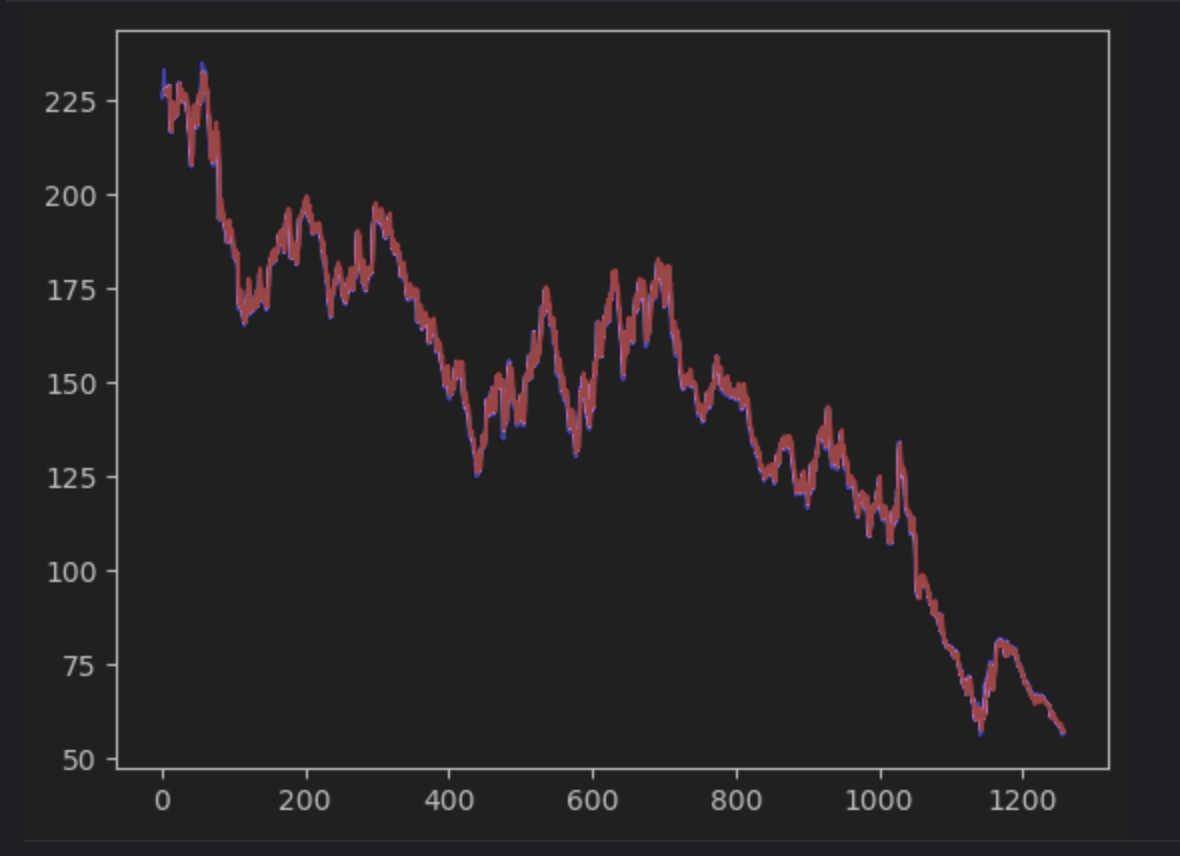
Si vous observez attentivement, vous verrez que les valeurs de la prévision et les valeurs réelles ne correspondent pas exactement. Toutefois, la plupart des prévisions sont remarquablement proches.
Pour inspecter les erreurs de façon plus précise, nous allons créer une série d’erreurs et utiliser le tableau interactif pour les observer. Nous utilisons l’erreur absolue cette fois-ci.
error = abs(timeseries-pred_series) error
Utilisez les paramètres pour créer un histogramme avec la valeur de l’erreur absolue comme axe des x et le nombre d’occurrences comme axe des y.
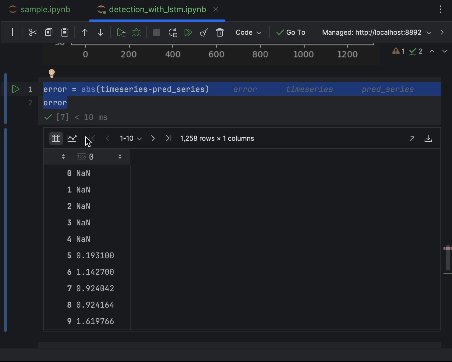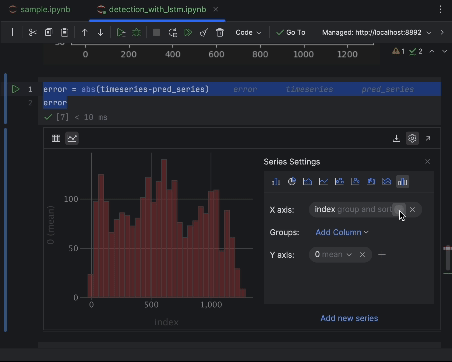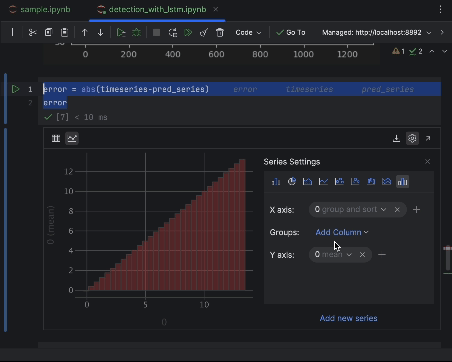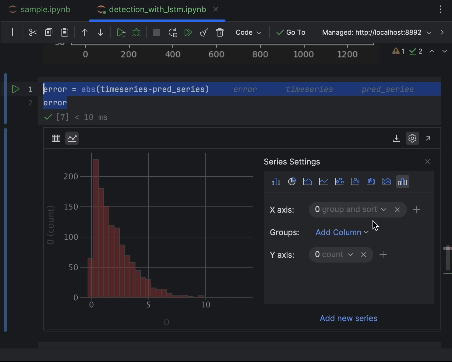
6. Décider du seuil d’anomalie et visualiser
La plupart des points auront une erreur absolue inférieure à 6, ce que nous allons utiliser comme seuil d’anomalie. Comme nous l’avons fait pour les anomalies de la ruche, nous pouvons tracer les points de données anormaux dans le graphique.
threshold = 6
error_series = pd.Series(error.flatten())
price_series = pd.Series(timeseries.flatten())
anomalies_filter = error_series.apply(lambda x: True if x > threshold else False)
anomalies = price_series[anomalies_filter]
plt.figure(figsize=(14, 8))
plt.scatter(x=anomalies.index, y=anomalies, color="red", label="anomalies")
plt.plot(df.index, timeseries, color='blue')
plt.title('Closing price')
plt.xlabel('Days')
plt.ylabel('Price')
plt.legend()
plt.show()
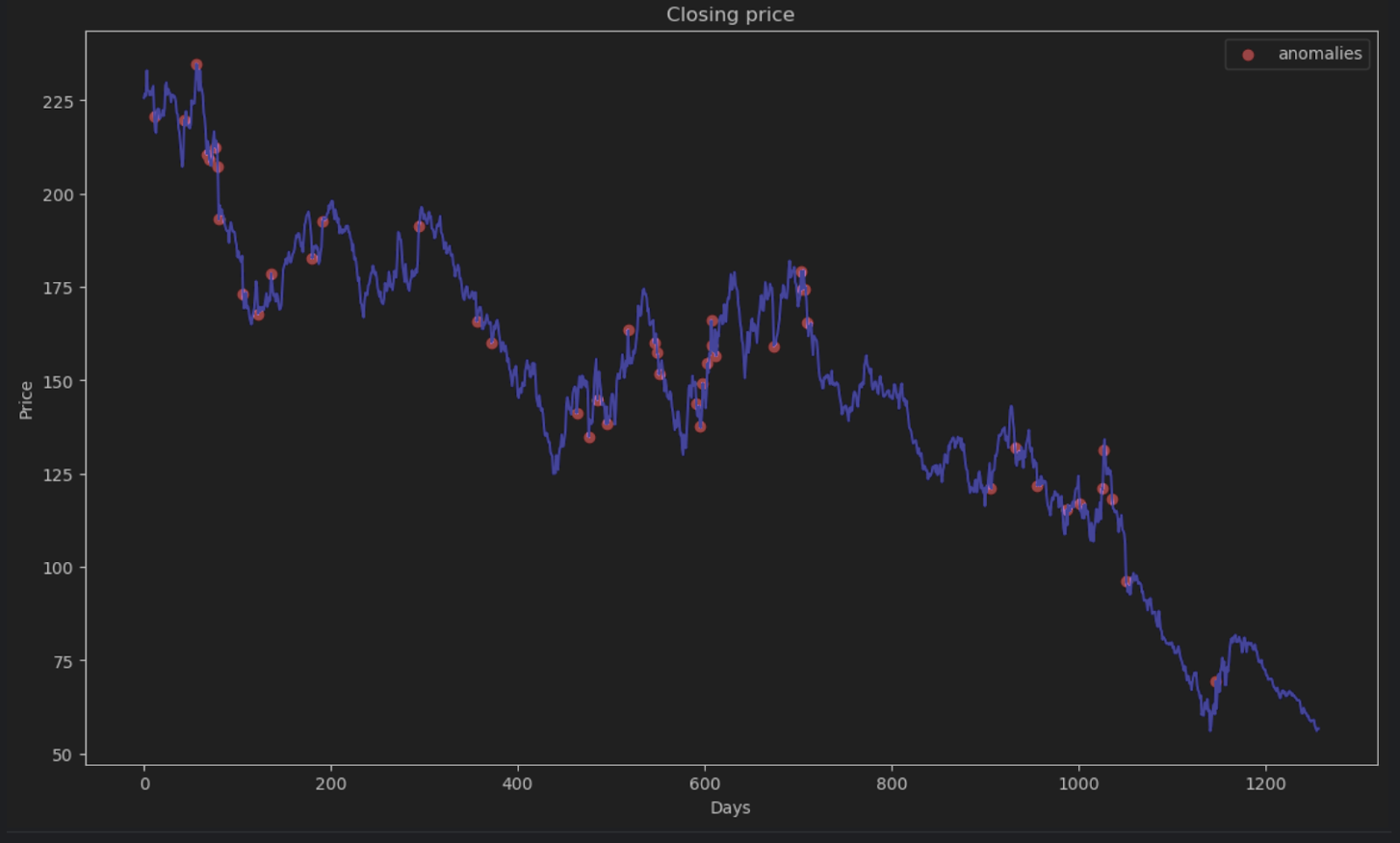
En résumé
Les séries chronologiques sont très fréquentes dans de nombreuses applications, notamment commerciales ou de recherche scientifique. En raison de la nature séquentielle des séries chronologiques, des méthodes et des algorithmes spéciaux sont employés pour y déterminer les anomalies. Dans cet article de blog, nous avons vu comment identifier les anomalies avec la décomposition STL pour éliminer la saisonnalité et les tendances. Nous avons également vu comment utiliser le deep learning et le modèle LSTM pour comparer l’estimation prévue et les données réelles pour déterminer les anomalies.
Détecter les anomalies avec PyCharm
Le projet Jupyter de PyCharm Professional permet d’organiser facilement votre projet de détection d’anomalie avec de nombreux fichiers de données et notebooks. La génération de graphiques permet d’inspecter les anomalies, d’autant plus que les tracés sont très accessibles dans PyCharm. D’autres fonctionnalités, telles que les suggestions de saisie semi-automatique, permettent de naviguer tous les modèles Scikit-learn et les paramètres de traçage Matplotlib très facilement.
Boostez vos projets de science des données en utilisant PyCharm et découvrez les fonctionnalités de science des données offertes pour simplifier votre workflow de science des données.
Auteur de l’article original en anglais :
Subscribe to PyCharm Blog updates







