Idiomatic Kotlin: Solving Advent of Code Puzzles, Working With Lists

Svetlana Isakova

This post continues our “Idiomatic Kotlin” series and provides the solution for the Advent of Code Day 9* challenge. While solving it, we’ll look into different ways to manipulate lists in Kotlin.

Day 9. Encoding error, part I

We need to attack a weakness in data encrypted with the eXchange-Masking Addition System (XMAS)! The data is a list of numbers, and we need to find the first number in the list (starting from the 26th) that is not the sum of any 2 of the 25 numbers before it. We’ll call the number valid if it can be presented as a sum of two numbers from the previous sublist, and invalid otherwise. Two numbers that sum to a valid number must be different from each other.

If the first 25 numbers are 1 through 25 in a random order, the next number must be the sum of two of those numbers to be valid:

• 26 would be a valid next number, as it could be 1 plus 25 (or many other pairs, like 2 and 24).
• 49 would be a valid next number, as it is the sum of 24 and 25.
• 100 would not be valid; no two of the previous 25 numbers sum to 100.
• 50 would also not be valid; although 25 appears in the previous 25 numbers, the two numbers in the pair must be different.

Solution, part I

Let’s solve the task in Kotlin! For a start, let’s implement a function that checks whether a given list contains a pair of numbers that sum up to a given number. We’ll later use this function to check whether a given number is valid by passing this number and the list of the previous 25 numbers as arguments.

For convenience, we can define the function as an extension on a List of Long numbers. We need to iterate over all the elements in the list, looking for the two with the given sum. The first naive attempt will be using forEach (we call it on this implicit receiver, our list of numbers) to iterate through the elements twice:

fun List<Long>.hasPairOfSumV1(sum: Long): Boolean {
   forEach { first ->
       forEach { second ->
           if (first + second == sum) return true
       }
   }
   return false
}
fun main() {
   val numbers = listOf(1L, 24, 25, 10, 13)
   println(numbers.hasPairOfSumV1(26)) // true; 26 = 1 + 25
   println(numbers.hasPairOfSumV1(49)) // true; 49 = 24 + 25
   println(numbers.hasPairOfSumV1(100)) // false

   // This is wrong:
   println(numbers.hasPairOfSumV1(50)) // true; 50 = 25 * 2
}

But this solution is wrong! Using this approach, first and second might refer to the same element. But as we remember from the task description, two numbers that sum to a valid number must be different from each other.

To fix that, we can iterate over a list of elements with indices and make sure that the indices of two elements are different:

fun List<Long>.hasPairOfSumV2(sum: Long): Boolean {
   forEachIndexed { i, first ->
       forEachIndexed { j, second ->
           if (i != j && first + second == sum) return true
       }
   }
   return false
}
fun main() {
   val numbers = listOf(1L, 24, 25, 10, 13)
   println(numbers.hasPairOfSumV2(50)) // false
}

This way, if first and second both refer to 25, they have the same indices, so they are no longer interpreted as a correct pair.

We can rewrite this code and delegate the logic for finding the necessary element to Kotlin library functions. For this case, any does the job. It returns true if the list contains an element that satisfies the given condition:

//sampleStart
fun List<Long>.hasPairOfSum(sum: Long): Boolean =
   indices.any { i ->
       indices.any { j ->
           i != j && this[i] + this[j] == sum
       }
   }
//sampleEnd

fun main() {
   val numbers = listOf(1L, 24, 25, 10, 13)
   println(numbers.hasPairOfSum(50)) // false
}

Our final version of the hasPairOfSum function uses any to iterate through indices instead of elements and checks for a pair that meets the condition. indices is an extension property on Collection that returns an integer range of collection indices, 0..size - 1; we call it on this implicit receiver, our list of numbers.

Finding an invalid number

Let’s implement a function that looks for an invalid number, one that is not the sum of two of the 25 numbers before it.

Before we start, let’s store the group size, 25, as a constant. We have a sample input that we can check our solution against which uses the group size 5 instead, so it’s much more convenient to change this constant in one place:

const val GROUP_SIZE = 25

We define the group size as const val and make it a compile-time constant, which means it’ll be replaced with the actual value at compile time. Indeed, if you use this constant (e.g. in a range GROUP_SIZE..lastIndex) and look at the bytecode, you’ll no longer be able to find the GROUP_SIZE property. Its usage will have been replaced with the constant 25.

For convenience, we can again define the findInvalidNumber function as an extension function on List. Let’s first implement it more directly, and then rewrite it using the power of standard library functions.

We use the example provided with the problem, where every number but one is the sum of two of the previous 5 numbers; the only number that does not follow this rule is 127:

//sampleStart
const val GROUP_SIZE = 5

fun List<Long>.findInvalidNumberV1(): Long? {
   for (index in (GROUP_SIZE + 1)..lastIndex) {
       val prevGroup = subList(index - GROUP_SIZE, index)
       if (!prevGroup.hasPairOfSum(sum = this[index])) {
           return this[index]
       }
   }
   return null
}

fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576)
   println(numbers.findInvalidNumberV1()) // 127
}
//sampleEnd

fun List<Long>.hasPairOfSum(sum: Long): Boolean =
   indices.any { i ->
       indices.any { j ->
           i != j && this[i] + this[j] == sum
       }
   }

Because we need to find the first number in the input list that satisfies our condition starting from the 26th, we iterate over all indices starting from GROUP_SIZE + 1 up to the last index, and for each corresponding element check whether it’s invalid. prevGroup contains exactly GROUP_SIZE elements, and we run hasPairOfSum on it, providing the current element as the sum to check. If we find an invalid element, we return it.

You may think that the sublist() function creates the sublists and copies the list content, but it doesn’t! It merely creates a view. By using it, we avoid having to create many intermediate sublists!

We can rewrite this code using the firstOrNull library function. It finds the first element that satisfies the given condition. This allows us to find the index of the invalid number. Then we use let to return the element staying at the found position:

const val GROUP_SIZE = 5
//sampleStart
fun List<Long>.findInvalidNumberV2(): Long? =
   ((GROUP_SIZE + 1)..lastIndex)
       .firstOrNull { index ->
           val prevGroup = subList(index - GROUP_SIZE, index)
           !prevGroup.hasPairOfSum(sum = this[index])
       }
       ?.let { this[it] }
//sampleEnd

fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576)
   println(numbers.findInvalidNumberV2()) // 127
}

fun List<Long>.hasPairOfSum(sum: Long): Boolean =
   indices.any { i ->
       indices.any { j ->
           i != j && this[i] + this[j] == sum
       }
   }

Note how we use safe access together with let to transform the index if one was found. Otherwise null is returned.

Using ‘windowed’

To improve readability, we can follow a slightly different approach. Instead of iterating over indices by hand and constructing the necessary sublists, we use a library function that does the job for us.

The Kotlin standard library has the windowed function, which returns a list or a sequence of snapshots of a window of a given size. This window “slides” along the given collection or sequence, moving by one element each step:

fun main() {
   val list = listOf('a', 'b', 'c', 'd', 'e')
   println(list.windowed(2)) // [[a, b], [b, c], [c, d], [d, e]]
   println(list.windowed(3)) // [[a, b, c], [b, c, d], [c, d, e]]
}

Here we build sublists, that is, snapshots, of size 2 and 3. To see more examples of how to use windowed and other advanced operations on collections, check out this video.

This function is perfectly suited to our challenge, as it can build sublists of the required size automatically for us. Let’s rewrite findInvalidNumber once more:

const val GROUP_SIZE = 5
//sampleStart
fun List<Long>.findInvalidNumberV3(): Long? =
    windowed(GROUP_SIZE + 1)
       .firstOrNull { window ->
           val prevGroup = window.dropLast(1)
           !prevGroup.hasPairOfSum(sum = window.last())
       }
       ?.last()
//sampleEnd

fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576)
   println(numbers.findInvalidNumberV3()) // 127
}

fun List<Long>.hasPairOfSum(sum: Long): Boolean =
   indices.any { i ->
       indices.any { j ->
           i != j && this[i] + this[j] == sum
       }
   }

To have both the previous group and the current number, we use a window with the size GROUP_SIZE + 1. The first GROUP_SIZE elements form the necessary sublist to check, while the last element is the current number. If we find a sublist that satisfies the given condition, its last element is the result.

Note about the difference between sublist and windowed functions

Note, however, that unlike sublist(), which creates a view of the existing list, the windowed() function builds all the intermediate lists. Though using it improves readability, it results in some performance drawbacks. For parts of the code that are not performance-critical, these drawbacks usually are not noticeable. On the JVM, the garbage collector is very effective at collecting such short-lived objects. It’s nevertheless useful to know about these nuanced differences between the two functions!

There’s also an overloaded version of the windowed() function that takes lambda as an argument describing how to transform each window. This version doesn’t create new sublists to pass as lambda arguments. Instead, it passes “ephemeral” sublists (somewhat similar to sublist() views) that are valid only inside the lambda. You should not store such a sublist or allow it to escape unless you’ve made a snapshot of it:

fun main() {
   val list = listOf('a', 'b', 'c', 'd', 'e')
   // Intermediate lists are created:
   println(list.windowed(2).map { it.joinToString("") })

   // Lists passed to lambda are "ephemeral",
   // they are only valid inside this lambda:
   println(list.windowed(2) { it.joinToString("") })

   // You should make a copy of a window sublist
   // to store it or pass further:
   var firstWindowRef: List<Char>? = null
   var firstWindowCopy: List<Char>? = null
   list.windowed(2) {
       if (it.first() == 'a') {
           firstWindowRef = it // Don't do this!
           firstWindowCopy = it.toList()
       }
       it.joinToString("")
   }
   println("Ref: $firstWindowRef")   // [d, e]
   println("Copy: $firstWindowCopy") // [a, b]
}

If you try to store the very first window [a, b] by copying the reference, you see that by the end of the iterations this reference contains different data, the last window. To get the first window, you need to copy the content.

A function with similar optimization might be added in the future for Sequences, see KT-48800 for details.

We can further improve our findInvalidNumber function by using sequences instead of lists. In Kotlin, Sequence provides a lazy way of computation. In the current solution, windowed eagerly returns the result, the full list of windows. If the required element is found in the very first list, it’s not efficient. The change to Sequence causes the result to be evaluated lazily, which means the snapshots are built only when they’re actually needed.

The change to sequences only requires one line. We convert a list to a sequence before performing any further operations:

const val GROUP_SIZE = 5
//sampleStart
fun List<Long>.findInvalidNumber(): Long? =
    asSequence()
       .windowed(GROUP_SIZE + 1)
       .firstOrNull { window ->
           val prevGroup = window.dropLast(1)
           !prevGroup.hasPairOfSum(sum = window.last())
       }
       ?.last()
//sampleEnd

fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576)
   println(numbers.findInvalidNumber()) // 127
}

fun List<Long>.hasPairOfSum(sum: Long): Boolean =
   indices.any { i ->
       indices.any { j ->
           i != j && this[i] + this[j] == sum
       }
   }

That’s it! We’ve improved the solution from the very first version, making it more “idiomatic” along the way.

The last thing to do is to get the result for our challenge. We read the input, convert it to a list of numbers, and display the invalid one:

fun main() {
   val numbers = File("src/day09/input.txt")
       .readLines()
       .map { it.toLong() }

   val invalidNumber = numbers.findInvalidNumber()
   println(invalidNumber)
}

For the sample input, the answer is 127, and for real input, the answer is also correct! Let’s now move on to solve the second part of the task.

Encoding error, part II

The second part of the task requires us to use the invalid number we just found. We need to find a contiguous set of at least two numbers in the list which sum up to this invalid number. The result we are looking for is the sum of the smallest and largest number in this contiguous range.

For the sample list, we need to find a contiguous list which sums to 127:

35 20 15 25 47 40 62 55 65 95 102 117 150 182 127 219 299 277 309 576

In this list, adding up all of the numbers from 15 through 40 produces 127. To find the result, we add together the smallest and largest number in this contiguous range; in this example, these are 15 and 47, producing 62.

Solution, part II

We need to find a sublist in a list with the given sum of its elements. Let’s first implement this function in a straightforward manner, then rewrite the same logic using library functions. We’ll discuss whether the windowed function from the previous part can help us here as well, and finally we’ll identify a more efficient solution.

To check the sum of every contiguous sublist of a given list, we try all the options for the list’s start and end indices, build each sublist, and calculate its sum. fromIndex belongs to a full range of indices, while toIndex should be greater than fromIndex and shouldn’t exceed the list size (the toIndex argument defines an exclusive, not inclusive, upper bound):

fun List<Long>.findSublistOfSumV1(targetSum: Long): List<Long>? {
   for (fromIndex in indices) {
       for (toIndex in (fromIndex + 1)..size) {
           val subList = subList(fromIndex, toIndex)
           if (subList.sum() == targetSum) {
               return subList
           }
       }
   }
   return null
}

fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576
   )
   println(numbers.findSublistOfSumV1(127)) // [15, 25, 47, 40]
}

We can rewrite this logic using the firstNotNullOfOrNull function. Here, we iterate over possible values for fromIndex and for toIndex and look for the first value that satisfies the given condition:

//sampleStart
fun List<Long>.findSublistOfSumV2(targetSum: Long): List<Long>? =
   indices.firstNotNullOfOrNull { fromIndex ->
       ((fromIndex + 1)..size)
           .firstNotNullOfOrNull { toIndex ->
               subList(fromIndex, toIndex).takeIf { it.sum() == targetSum }
           }
   }

//sampleEnd
fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576
   )
   println(numbers.findSublistOfSumV2(127)) // [15, 25, 47, 40]
}

The logic hasn’t changed, we’ve simply rewritten it using the firstNotNullOfOrNull. If a sublist with the required sum is found, it’s returned from both firstNotNullOfOrNull calls as the first found non-null value.

The takeIf function returns its receiver if it satisfies the given condition or null if it doesn’t. In this case, the takeIf call returns the found sublist if the sum of its elements is equal to the provided targetSum.

An alternative way to solve this problem is, for each possible sublist size, to build all the sublists of this size using the windowed function, and then check the sum of its elements:

//sampleStart
fun List<Long>.findSublistOfSumV3(targetSum: Long): List<Long>? =
   (2..size).firstNotNullOfOrNull { sublistSize ->
       asSequence()
           .windowed(sublistSize)
           .firstOrNull { sublist ->
               sublist.sum() == targetSum
           }
   }

//sampleEnd
fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576
   )
   println(numbers.findSublistOfSumV3(127)) // [15, 25, 47, 40]
}

As before, we convert the input list to a sequence to perform the operation in a lazy manner: each new sublist is created when it needs to be checked for sum.

All the functions we’ve considered so far work for the challenge input and give the correct answer, but they have one common disadvantage: they manipulate the sublists of all possible sizes, and for each one, calculate the sum. This approach isn’t the most efficient. We can do better, can’t we?

We can precalculate all the sums of sublists from the first element in the list to each element, and use these “prefix” sums to easily calculate the sum between any two elements. If we have the sum of elements from 0 to fromIndex, and the sum of elements from 0 to toIndex, the sum of the elements from fromIndex to toIndex can be found by subtracting the former from the latter:

sum(fromIndex, toIndex) = sum(0, toIndex) - sum(0, fromIndex)

The following illustration shows that:

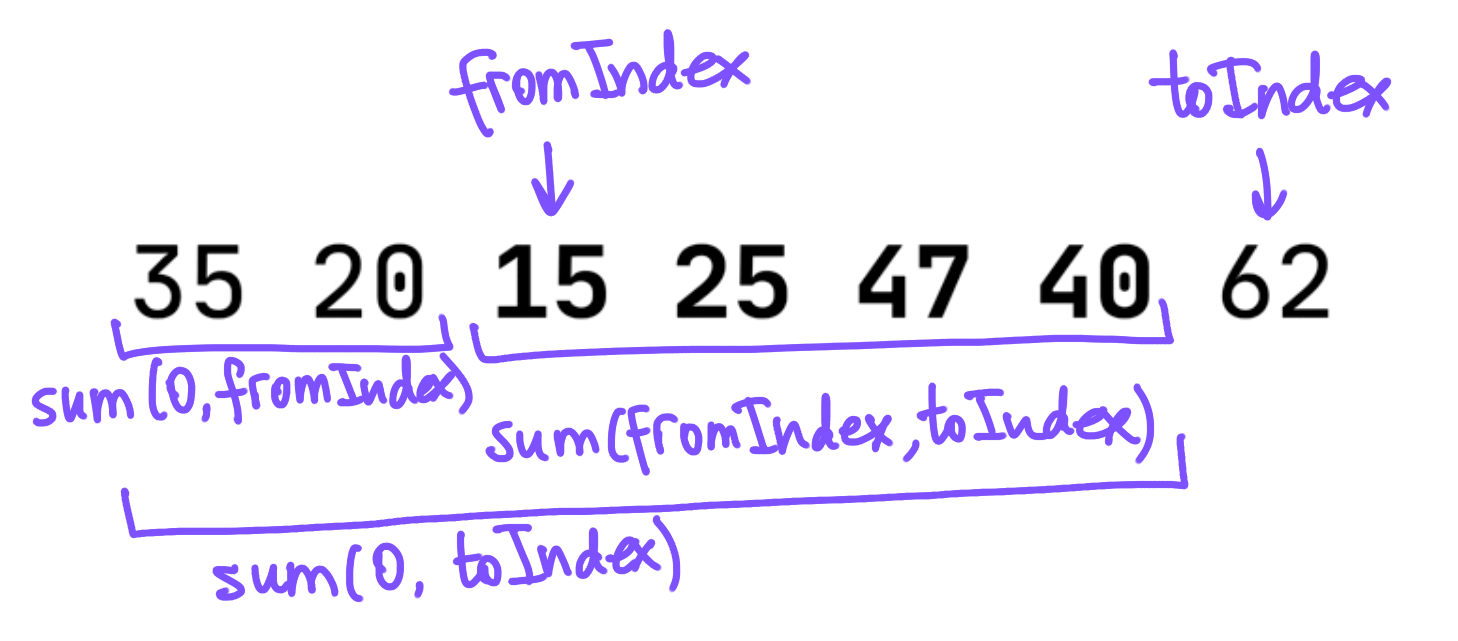
We need to precalculate the prefix sum for each element. We can use the standard library’s scan function for that! It also has another name, runningFold.

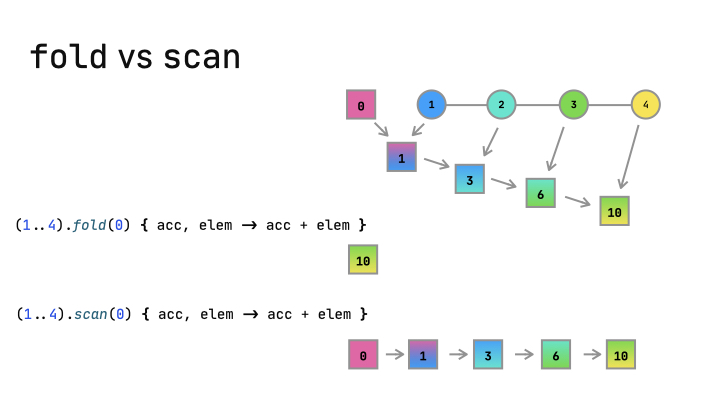
The fold and scan (runningFold) functions are related:

• They both “accumulate” value starting with the initial value. On each step, they apply the provided operation to the current accumulator value and the next element.
• fold returns only the final result, while scan (runningFold) returns the results for all the intermediate steps.

fun main() {
   println((1..4).fold(0) { acc, elem -> acc + elem }) // 10
   println((1..4).scan(0) { acc, elem -> acc + elem }) // [0, 1, 3, 6, 10]
}

The following animation illustrates the fold and scan functions in action:

After precalculating all the prefix sums, we use them to find the sums of all the possible sublists, and look for the required sum:

//sampleStart
fun List<Long>.findSublistOfSum(targetSum: Long): List<Long>? {
   val prefixSums = scan(0L) { acc, element -> acc + element }
   return indices.firstNotNullOfOrNull { fromIndex ->
       ((fromIndex + 1)..size).firstNotNullOfOrNull { toIndex ->
           val subListSum = prefixSums[toIndex] - prefixSums[fromIndex]
           if (subListSum == targetSum) subList(fromIndex, toIndex) else null
       }
   }
}
//sampleEnd
fun main() {
   val numbers = listOf<Long>(
       35, 20, 15, 25, 47, 40, 62,
       55, 65, 95, 102, 117, 150, 182,
       127, 219, 299, 277, 309, 576
   )
   println(numbers.findSublistOfSum(127)) // [15, 25, 47, 40]
}

In this solution, we explicitly build only one sublist of the required sum to return it as the result.

Let’s now call the findSublistOfSum function to find the result for our initial challenge. After we found the invalid number in part I, we pass this value as an argument to the findSublistOfSum function, and then find the sum of the minimum and maximum values of the resulting list:

fun main() {
   val numbers = File("src/day09/input.txt")
       .readLines()
       .map { it.toLong() }

   val invalidNumber = numbers.findInvalidNumber()
       ?: error("All numbers are valid!")
   println("Invalid number: $invalidNumber")

   val sublist = numbers.findSublistOfSum(sum = invalidNumber)
       ?: error("No sublist is found!")
   println(sublist.minOf { it } + sublist.maxOf { it })
}

Note how we use the error function to report an error and throw an exception in the event that one of our functions returns null. In AdventOfCode puzzles, we assume that the input is correct, but it’s still useful to handle errors properly.

That’s all! We’ve discussed the solution for the Day 9 AdventOfCode challenge and worked with the any, firstOrNull, firstNotNullOfOrNull, windowed, takeIf and scan functions, which exemplify a more idiomatic Kotlin style.

—

*Used with the permission of Advent of Code (Eric Wastl).

Subscribe to Kotlin Blog updates

Subscribe form

By submitting this form, I agree to the JetBrains Privacy Policy Notification icon

By submitting this form, I agree that JetBrains s.r.o. ("JetBrains") may use my name, email address, and location data to send me newsletters, including commercial communications, and to process my personal data for this purpose. I agree that JetBrains may process said data using third-party services for this purpose in accordance with the JetBrains Privacy Policy. I understand that I can revoke this consent at any time in my profile. In addition, an unsubscribe link is included in each email.

Submit

Thanks, we've got you!