Multik 0.1 Is Out

Pavel Gorgulov

Introducing Multik 0.1 – a new, enhanced version of our multidimensional array library! You can check out the previous post to learn about the basic features and architecture of the library.

In the new release, we added new methods from linear algebra, supported complex numbers and reading/writing .csv files, improved the performance and stability of existing functions, and added many more features that will make it easier for you to work with multidimensional arrays.

Multik on GitHub

Let’s take a look at the new features this release brings to the API:

• Reading and writing CSV files
• Complex numbers
• LU factorization
• Solving linear systems
• Inverse matrix
• QR factorization
• Eigenvalues and eigenvectors
• Append, stack, and meshgrid

Reading and writing CSV files

CSV is a popular data recording format, and now Multik 0.1 allows you to read and write .csv files easily.

val a = mk.d2array(2, 2) { it }
mk.write("example.csv", a)
val b = mk.read<Int, D2>("example.csv")
println(b)
/*
[[0, 1],
[2, 3]]
*/

Complex numbers

Complex numbers are expressed as re + i ∙ im, where re and im are real numbers and i is the imaginary unit equal to the square root of -1; re is the real part of the complex number and i ∙ im is the imaginary part. Complex numbers are common in algebra and are now a part of the Multik API.

val cf = ComplexFloat(1f, 2f) // 1.0+(2.0)i
val cd = ComplexDouble.one // 1.0+(0.0)i

The ComplexFloat and ComplexDouble classes are created in full accordance with the Number classes, so there is no need to learn a new API.

val c1 = ComplexFloat(1f, 2f) // 1.0+(2.0)i
val c2 = ComplexFloat(3f, 4f) // 3.0+(4.0)i

println(c1 + c2) // 4.0+(6.0)i
println(c1 * c2) // -5.0+(10.0)i

val (re, im) = c1 // re = 1.0; im = 2.0
val re2 = c2.re // 3.0
val im2 = c2.im // 4.0

We’ve also added ComplexFloatArrays and ComplexDoubleArrays. They support all methods that primitive arrays do, except for methods that use comparison, since complex numbers are unordered. But you can use methods such as minBy, maxBy, sortedBy, and others to define the comparison logic yourself.

val array = ComplexDoubleArray(5) { ComplexDouble(it, it.toDouble() / 2) }

println(array)
// [0.0 + 0.0i, 1.0 + 0.0i, 2.0 + 1.0i, 3.0 + 1.0i, 4.0 + 2.0i]

println(array.filter { it.abs() > 2.0 })
// [2.0+(1.0)i, 3.0+(1.5)i, 4.0+(2.0)i]

println(array.sortedByDescending { it.im })
// [4.0+(2.0)i, 3.0+(1.5)i, 2.0+(1.0)i, 1.0+(0.5)i, 0.0+(0.0)i]

After supporting complex numbers and arrays of complex numbers, we added them to multidimensional arrays.

println(mk.d2arrayIndices(2, 2) { i, j -> ComplexFloat(i, j) })
/*
[[0.0+(0.0)i, 0.0+(1.0)i],
[1.0+(0.0)i, 1.0+(1.0)i]]
 */

println(mk.empty<ComplexDouble, D1>(5))
// [0.0+(0.0)i, 0.0+(0.0)i, 0.0+(0.0)i, 0.0+(0.0)i, 0.0+(0.0)i]

println(mk.ndarrayOf(ComplexDouble.zero, ComplexDouble.one))
//[0.0+(0.0)i, 1.0+(0.0)i]

You can do everything with them that you did with integer and float multidimensional arrays before.

val ndarray = mk.d2arrayIndices(3, 3) { i, j -> ComplexDouble(i, j) }
println(ndarray.map { it.re * it.re + it.im * it.im })
/*
[[0.0, 1.0, 4.0],
[1.0, 2.0, 5.0],
[4.0, 5.0, 8.0]]
 */

 println(mk.math.sin(ndarray))
 /*
[[0.0+(0.0)i, 0.0+(1.1752011936438014)i, 0.0+(3.626860407847019)i],
[0.8414709848078965+(0.0)i, 1.2984575814159773+(0.6349639147847361)i, 3.165778513216168+(1.9596010414216063)i],
[0.9092974268256817+(-0.0)i, 1.4031192506220405+(-0.4890562590412937)i, 3.4209548611170133+(-1.5093064853236158)i]]
*/

We still have several open tasks for complex numbers. You can participate in the development of the library and become a contributor.

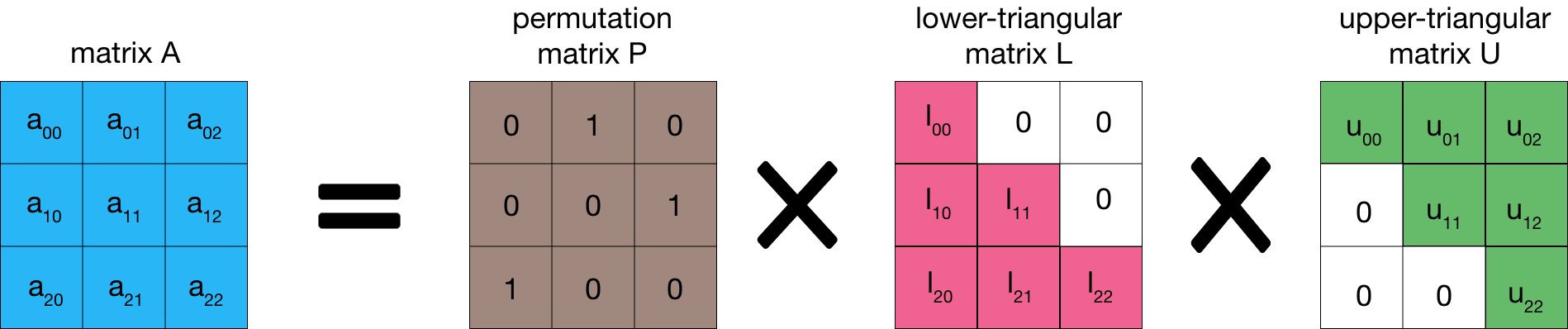
LU factorization

LU factorization, or lower-upper decomposition, represents a matrix as the product of a permutation matrix, a lower triangular matrix, and an upper triangular matrix: A = P ✕ L ✕ U.

We have Introduced this in Multik.

val a = mk.d2array(3, 3) { it.toDouble() }
val (p, l, u) = mk.linalg.plu(a)

abs((p dot l dot u) - a).all { 1e-13 > it } // true

Solving linear systems

Solving systems of linear equations is a common problem encountered in algebra. With PLU factorization, we can easily solve square linear systems. To do this, we have provided a corresponding method in linalg.

val a = mk.ndarray(mk[mk[2, 5, 1], mk[7, 3, 1], mk[8, 9, 4]])
val b = mk.ndarray(mk[3, 1, 2])
mk.linalg.solve(a, b)
// [-0.036363636363636265, 0.9090909090909091, -1.4727272727272729]

Inverse matrix

The inverse matrix of a square matrix A, denoted A-1, is such that the following equality holds: A ✕ A-1 = A-1 ✕ A = I, where I is the square identity matrix. If A-1 is nonsingular, then it can be calculated by solving the above expression. For convenience, we have added this method out of the box.

val a = mk.ndarray(mk[mk[2.0, 5.0, 1.0], mk[7.0, 3.0, 1.0], mk[8.0, 9.0, 4.0]])
val ainv = mk.linalg.inv(a)
abs((a dot ainv) - mk.identity<Double>(3)).all { 1e-13 > it } // true

QR factorization

Another important decomposition is QR decomposition. We can decompose any square matrix A as a product Q ✕ R, where Q is an orthogonal matrix and R is an upper triangular matrix.

val a = mk.d2array(3, 3) { (it * it).toDouble() }
val (q, r) = mk.linalg.qr(a)
abs(a - (q dot r)).all { 1e-13 > it } //  true

Eigenvalues and eigenvectors

Based on the QR decomposition, we’ve made it possible to calculate eigenvalues and eigenvectors with Multik.

val a = mk.ndarray(mk[mk[1, -1], mk[1, 1]])
val (w, v) = mk.linalg.eig(a)
/*
w = [0.9999999999999998+(0.9999999999999998)i, 1.0+(-0.9999999999999998)i]

v = 
[[0.7071067811865476+(0.0)i, 0.7071067811865474+(0.0)i],
[-0.0+(-0.7071067811865475)i, -8.326672684688674E-17+(0.7071067811865474)i]]
*/

Append, stack, and meshgrid

In this release, we have added functions to help you work with multidimensional arrays more easily.

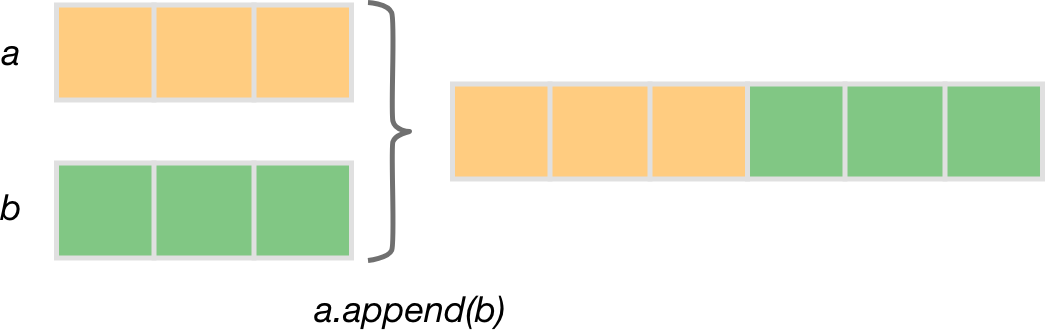
For example, you can use the append function to concatenate an array with scalars and other arrays. We’re grateful to our contributor Ansh Tyagi for implementing this feature.

val a = mk.d1array(5) { it }
a.append(10) // [0, 1, 2, 3, 4, 10]
a.append(mk.ndarrayOf(9, 8, 7)) // [0, 1, 2, 3, 4, 9, 8, 7]

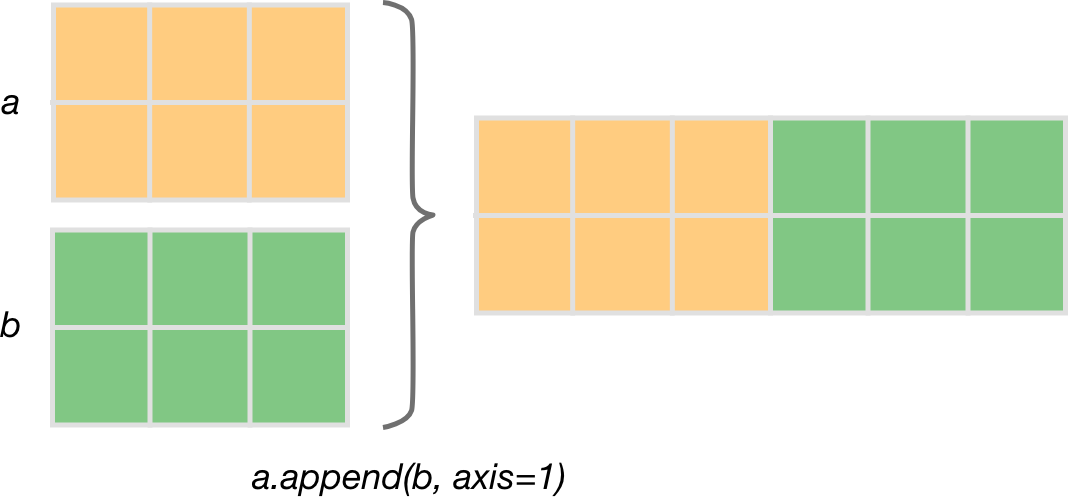
Append can also be used along the ndarray axes, which then becomes equivalent to cat function.

val a = mk.d2array(2, 3) { it }
println(a.append(a, axis=0))
/*
[[0, 1, 2],
[3, 4, 5],
[0, 1, 2],
[3, 4, 5]]
*/

println(a.append(a, axis=1))
/*
[[0, 1, 2, 0, 1, 2],
[3, 4, 5, 3, 4, 5]]
*/

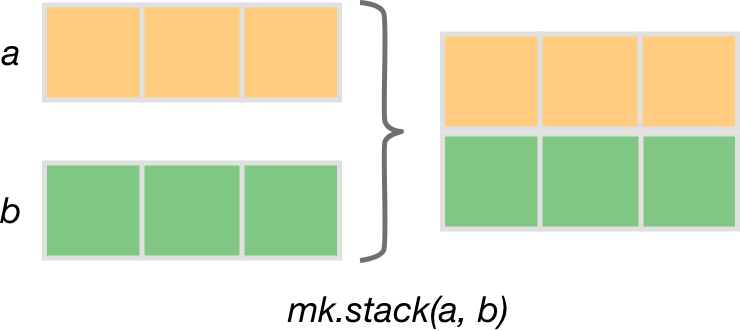
stack allows arrays to be concatenated along a new axis.

val a = mk.ndarrayOf(1, 2, 3)
println(mk.stack(a, a))
/*
[[1, 2, 3],
[1, 2, 3]]
*/

println(mk.stack(a, a, axis=1))
/*
[[1, 1],
[2, 2],
[3, 3]]
*/

And meshgrid allows you to get a grid of coordinates from vectors.

val x = mk.linspace<Double>(0, 1, 3)
val y = mk.linspace<Double>(0, 1, 4)
val (xg, yg) = mk.meshgrid(x, y)

println(xg)
/*
[[0.0, 0.5, 1.0],
 [0.0, 0.5, 1.0],
 [0.0, 0.5, 1.0],
 [0.0, 0.5, 1.0]]
 */

println(yg)
/*
[[0.0, 0.0, 0.0],
 [0.3333333333333333, 0.3333333333333333, 0.3333333333333333],
 [0.6666666666666666, 0.6666666666666666, 0.6666666666666666],
 [1.0, 1.0, 1.0]]
 */

Conclusion

For more details about this new release, please check out the changelog.

We want to thank our users and contributors – you help us improve the library and make it more reliable and convenient!

To use Multik in your project, add the following dependencies to your build.gradle file:

repositories {
    mavenCentral()
}

dependencies {
    implementation "org.jetbrains.kotlinx:multik-api:0.1.0"
    implementation "org.jetbrains.kotlinx:multik-default:0.1.0"
}

You can use different engines, not just the default. We have multik-default, multik-native, and multik-jvm. Please note that on Android we only support the JVM engine.

Alternatively, you can start using Multik in Jupyter or Datalore:

%use multik

If you don’t have the kotlin-kernel for Jupyter, you can read about installation here. In Datalore, everything works out of the box.

We’re looking for contributions from the community, so please don’t hesitate to join the effort! Current tasks can always be found in the issue tracker.

Try out Multik 0.1 and share your experience with us!

Let’s Kotlin!

Subscribe to Kotlin Blog updates

Subscribe form

By submitting this form, I agree to the JetBrains Privacy Policy Notification icon

By submitting this form, I agree that JetBrains s.r.o. ("JetBrains") may use my name, email address, and location data to send me newsletters, including commercial communications, and to process my personal data for this purpose. I agree that JetBrains may process said data using third-party services for this purpose in accordance with the JetBrains Privacy Policy. I understand that I can revoke this consent at any time in my profile. In addition, an unsubscribe link is included in each email.

Submit

Thanks, we've got you!