BeamSearch in code generation
In the previous article devoted to full-line code completion, we looked into the vocabulary that the neural net of our full line completion plugin uses for Python. However, just having 16384 tokens like self., or, s.append(, return value, and others described in the article is not enough to generate even a single line. We need a way to combine these tokens together to write chunks of code. In today’s article, we will discuss how the algorithm constructs longer phrases using the elements of the vocabulary.
The first idea that deserves mentioning is autoregression.
Autoregression
Autoregression is just one of the several concepts upon which text (and code) generation is based. The ML-based algorithms take the existing text, or part of it, as input, and predict the probability that each of the tokens from the vocabulary has of being the next token in the text.
The prediction of these probabilities is done by a Transformer-based neural net model. In this article, we will treat this model as a black box taking a sequence of tokens and returning the probabilities of the next possible token. There are many articles on how the neural net Transformers work that explain the inside of this black box. For example, see the original research paper about the Transformer or an illustrated explanation specifically devoted to GPT-2.
We’ll leave the Transformer implementation details out of this article’s scope. Instead, we’ll look into what the algorithm does once these probabilities are obtained.
We can take the most probable token and feed it back into the algorithm as a part of the context for the next inference iteration. This allows us to predict the second token in the sequence, which we can later use as a part of the context again. Therefore, only the first iteration uses input provided by the user, while all subsequent iterations combine that input with the results of the previous steps.
For starters, let’s try running these steps on an artificial natural language example. William Blake’s “The Tyger” will be the text we pretend to predict:

This example illustrates that the autoregressive process is potentially infinite. By adding more tokens to the end of the text and moving the context window forward, we can get to the situation where no part of the original text is used as input.
In real-life applications, the input is rarely a duplicate of an element from the training set. This means that the output is less clear and the attempts to generate long meaningful text result in much lower quality than Blake’s poem.
Fortunately, our immediate task is to generate only a small fragment of code, so we default the process to five iterations instead of infinity. Our model takes up to 384 tokens of context, so we don’t risk losing track of the original input when generating these five new tokens.
Results diversity and computational complexity
The straightforward autoregression has a problem: It generates only one chain of tokens. This may be fine when the model is highly confident and the combined probability of all the results except the top one is negligible. This is the case with “The Tyger,” where every next word is immediately obvious to anyone who memorized that poem at school.
In practice, many continuations are often possible, so we want to explore plenty of options. And this is where exponential complexity comes into play. Our vocabulary contains 214 == 16384 tokens, and the algorithm provides the probabilities for each of them. For the next step, where combinations of two tokens are considered, we already have 214 * 214 == 228 options. To “write” a sequence of five tokens, we need to select it from 270 variations, which is beyond reasonable. The search tree has too many branches to be fully traversed.
We need some way to do a breadth-first search but limit the computational power we spend on every level of the tree. There are several possible solutions, one of them being nucleus sampling. We, however, selected the algorithm named BeamSearch. The name suggests that we use a fixed-width laser-like beam of light to explore the landscape.
Practically that means selecting a fixed number of branches on each level of the tree for further exploration. We leave only those branches that seem most probable at the moment and cut everything else. Let’s see how it works with Python tokens.
BeamSearch
Let’s assume we start implementing a Python function calculating the nth Fibonacci number. The example we use might not be the brightest demonstration of AI power, but it allows us to show how we build something on top of hard-to-interpret probabilistic results obtained from the neural net. The first thing we want to do is check if the input value is negative and throw an exception—err, sorry, raise an error—if it is. Here’s how it works:
n = int(input())
def fib(n):
if n < 0:
rai| To understand how the algorithm composes its suggestions, we’ll use the information available to the plugin developers in debug mode.
Our beam is six items wide, meaning that the algorithm only selects the six most probable token combinations at each step. We will depict them as a graph. The line width will represent the relative probabilities of the continuations within the iteration.
The first step of the algorithm gives us the following results:

r” and the empty yellow rectangle at the bottom, which has the highest probability. What on Earth is this?The user may invoke the completion window anywhere in the code, and we need to find the best way to represent the prefix, i.e., the sequence between the line start and the invocation place, in terms of the vocabulary tokens. Sometimes the algorithm can cover the whole prefix with the first token it considers, but sometimes two or more tokens are needed.
We want to continue the line which consists of two indents and “rai”. So the two strange items mentioned above attempt to start from indent+indent+“r” or just indent+indent, both of which are tokens in the vocabulary.
So far so good. Let’s move on to the next step. We’ll switch back and forth between yellow and light blue to highlight the tokens that are used to compose the suggestions:
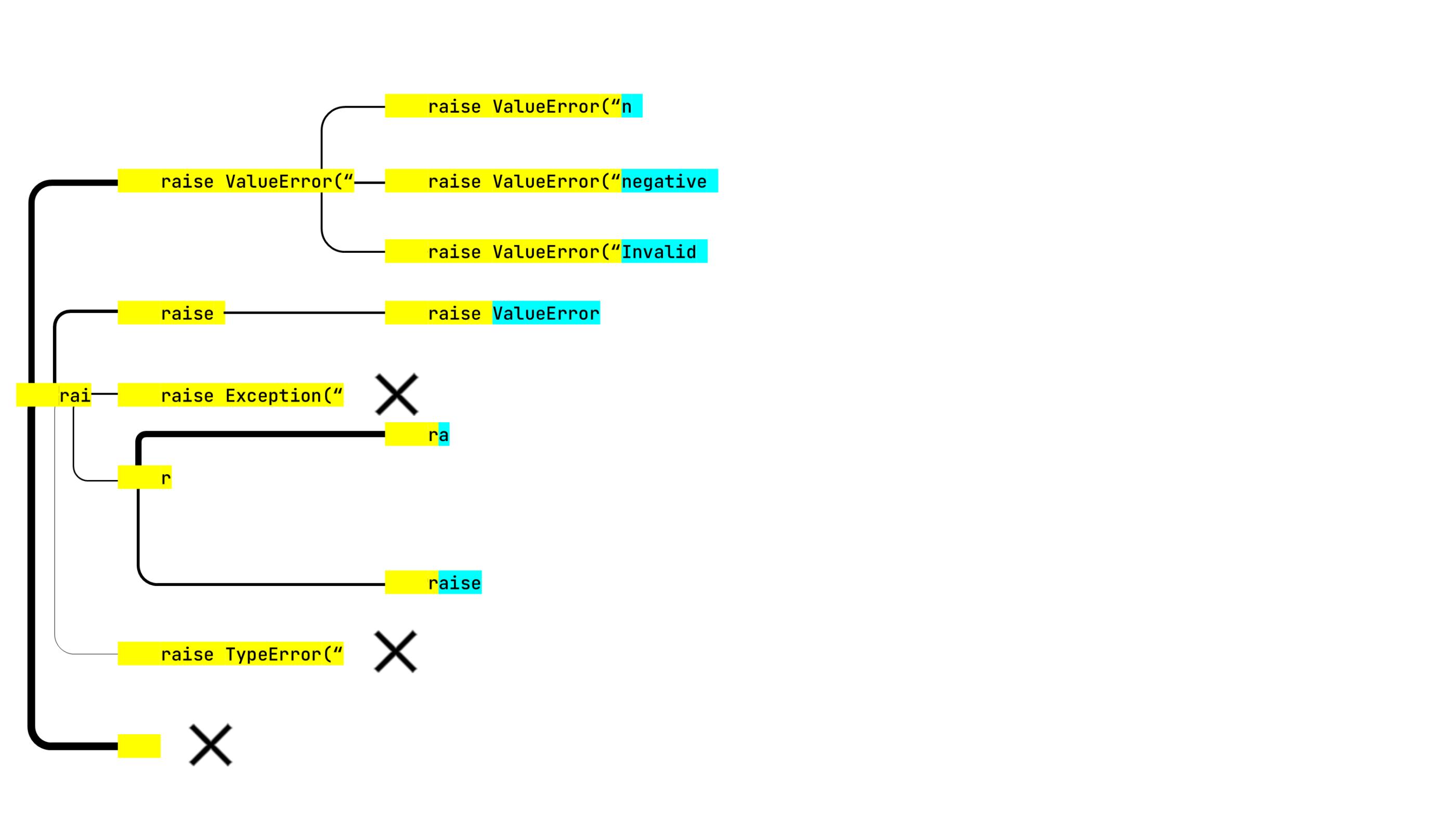
- There are many options that start with indent+indent, therefore the probability of that continuation was high on the first iteration. However, none of these options individually appeared good enough to beat the continuations built from other starting tokens. So the search stops exploring this line, and we mark it with a cross, together with two other options.
- Sometimes a longer string can be represented with one token, while its substring requires two or more of them. In this case, we obtained raise ValueError(“ on the previous step, but raise ValueError didn’t become available until the current step.
- The error message texts all look very promising. It’s a pity that the next step is where it all goes wrong:
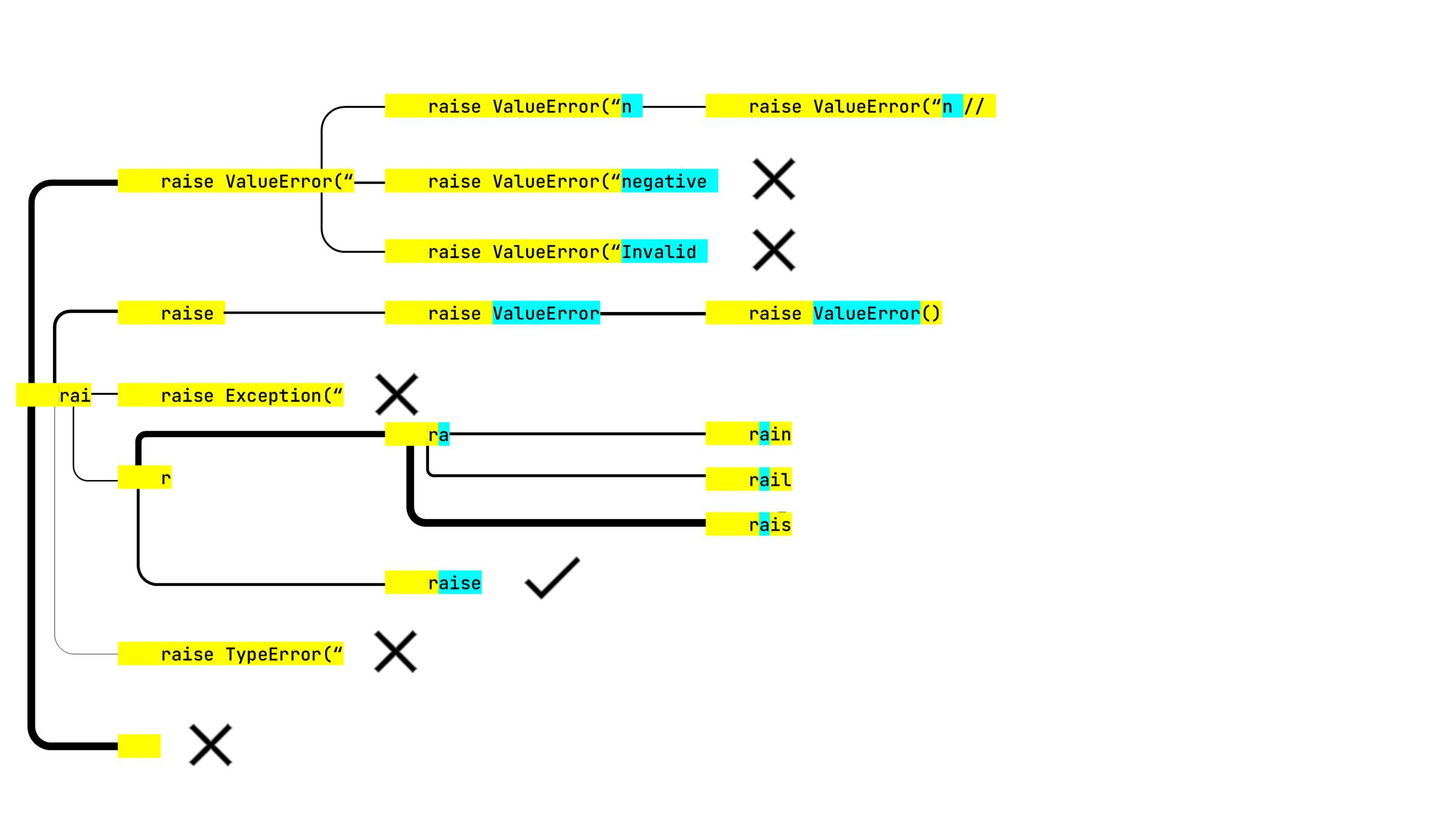
raise is a lexically correct chunk, so it can stop exploring this line. This analysis counts towards the six items on each step. That’s why there are only five other options.Unfortunately, we have also lost all the promising error messages on this step, but the other tree branch generated raise ValueError(), which is the next best thing. And we still have two more steps left to explore other possibilities. Rail? Rain? Rais? Let’s see.
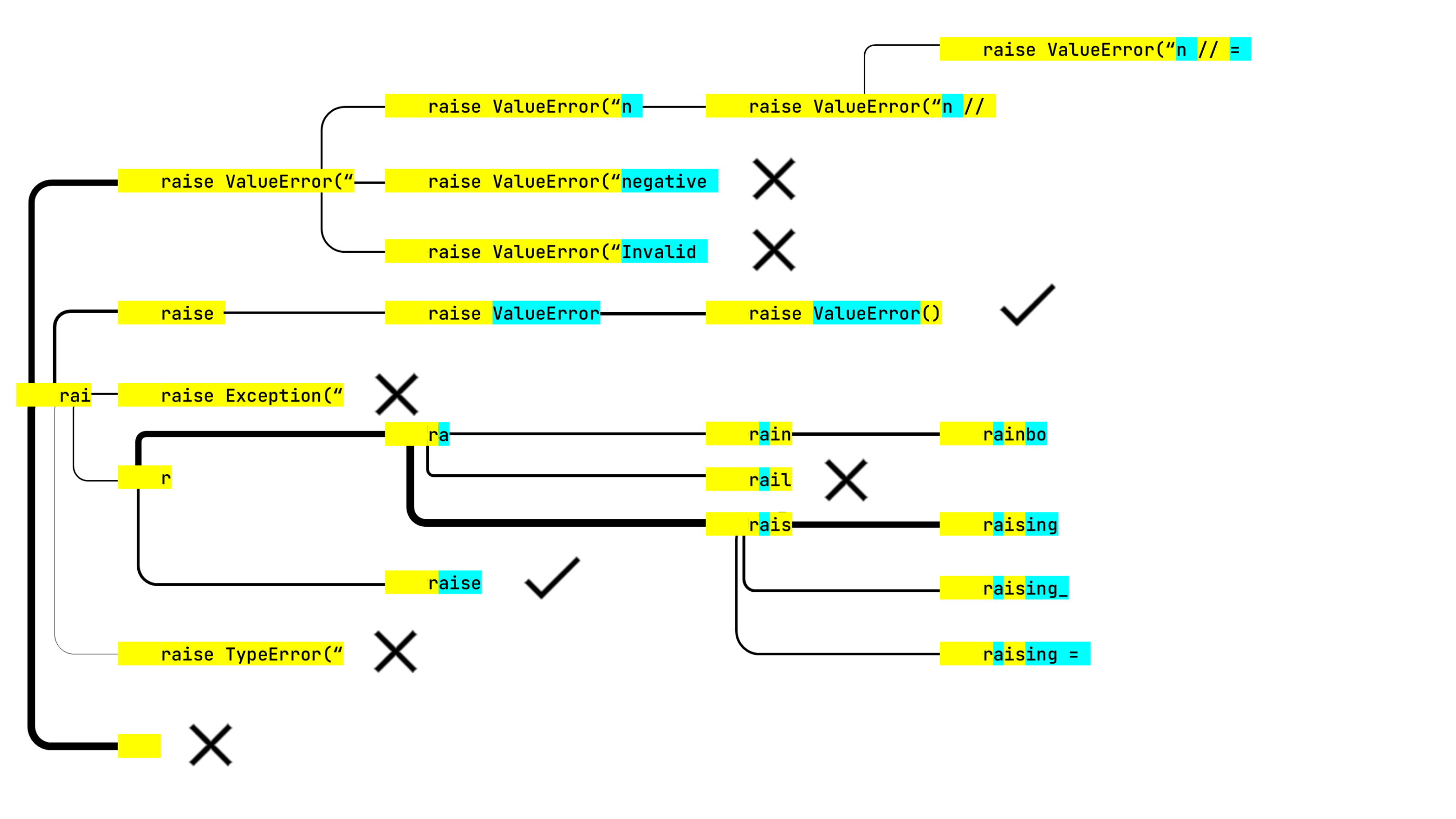
raise ValueError(“n // was an obvious dead end, but the neural net thought otherwise and continued building this line. On the plus side, raise ValueError() got checkmarked. The algorithm has five lines to analyze in the last step.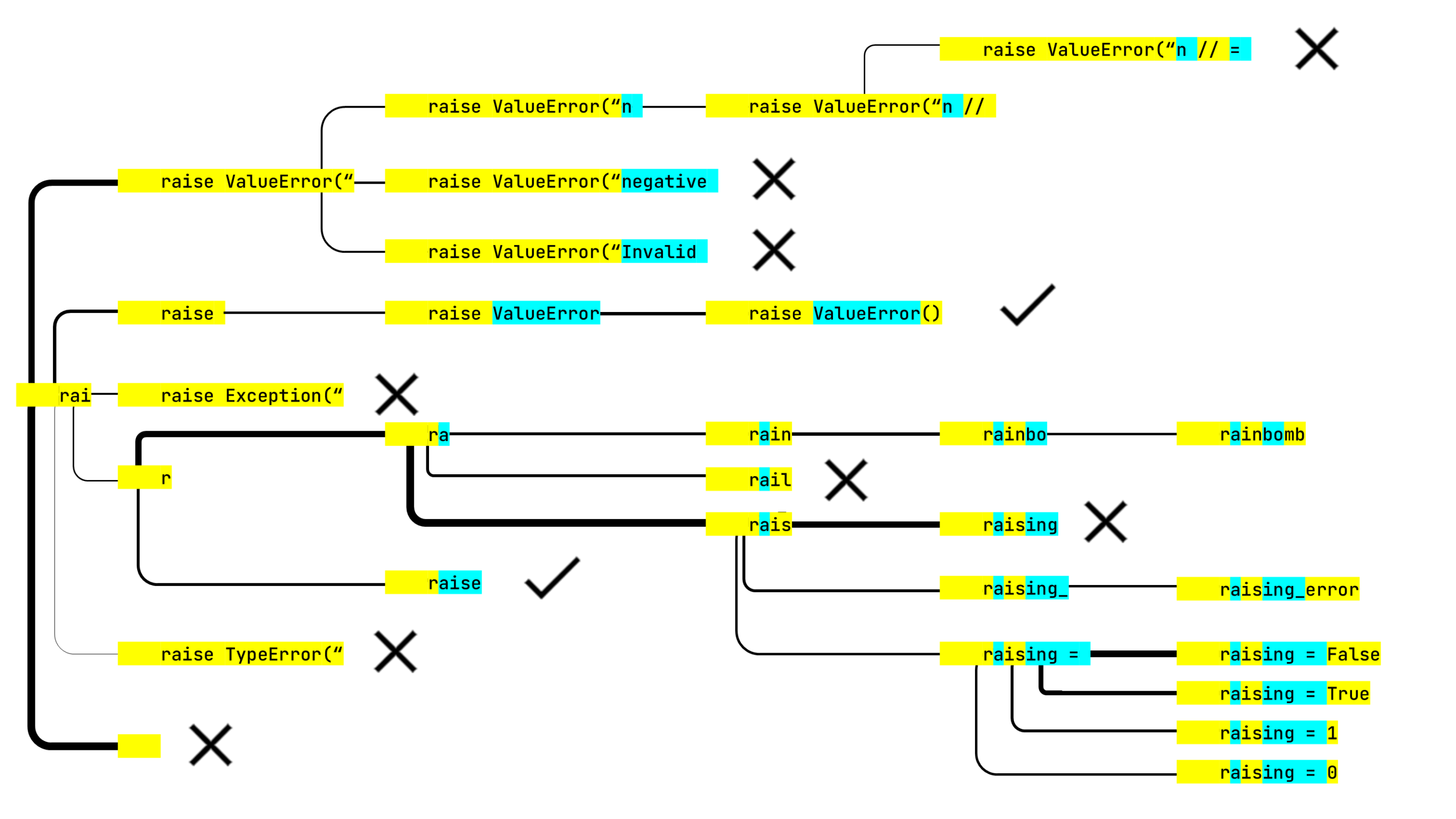
rainbo would lead to rainbow. The rainbomb we got instead was a surprise. Fortunately, the algorithm didn’t consider this option probable enough to show it to the users (other than the readers of this article).After all possible suggestions are generated, the algorithm sorts them by probability. In the near future, we plan to start boosting the lexically complete constructions of the target programming language, so that the brackets are balanced and the keywords are not split into parts.
However, we don’t want to fully suppress the partially incorrect suggestions. They may be just slightly incorrect, and it may be beneficial for the user to accept them and continue editing.
The specific pop-up used to write this explanation contained the following (what you see if you run the same code may differ depending primarily on available processor resources):
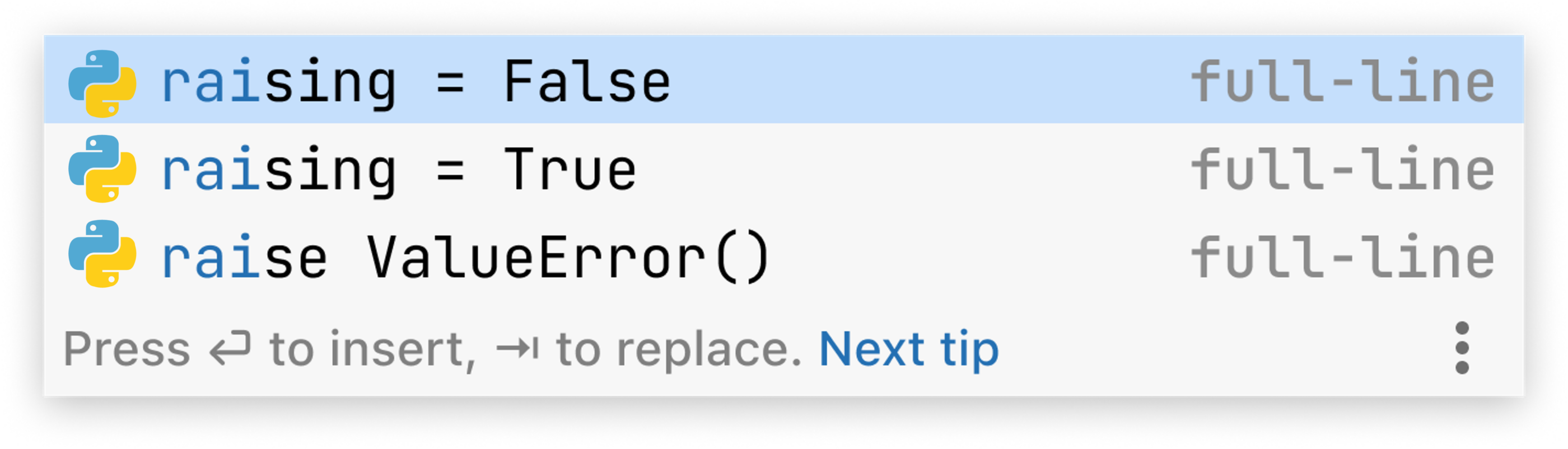
This might not look like unquestionable success, but still is a useful result for a developer implementing the fib(n) function.
The BeamSearch algorithm is a fairly simple way to limit the computational complexity of breadth-first search in a tree or graph. At the same time, it ensures a degree of diversity among the results.
To improve full line completion further…
…we need more feedback from our users. Please try the full line code completion plugin for Python and let us know what you think.
Subscribe to JetBrains Blog updates






