Dataflow Analysis of Integral Values

Maria Pashkova

Today we are introducing a new type of dataflow code analysis in ReSharper and Rider. We’ve gathered some statistics (by exploring the IL metadata of a large number of NuGet.org packages with an OSS license) and noticed that int is one of the most commonly used types for local variables.

That’s why this new analysis tracks the usage of values of the int type in your programs. It tracks the flow of integer values through your programs to detect useless or possibly erroneous pieces of code. It warns you about the following issues:

• Relational/equality operators that always evaluate to true or false.
• Unreachable switch cases checking int values.
• Meaningless arithmetic operations, such as multiplication by 1, addition of 0, etc.
• Possible int overflows.
• Possible division by 0.
• Possible errors in invocations of System.Math methods.

How it works

There are several different approaches to detecting issues associated with integer values. The method we’ve chosen is called abstract interpretation. In short, we interpret all statements and expressions in the program which can produce or affect integer values as part of static code analysis. We do not know the exact value of each variable, since most of them can be known only at runtime. However, we can collect some information about these values thanks to the int type constants used, literals, and arithmetic operations, and we can try to make use of this information.

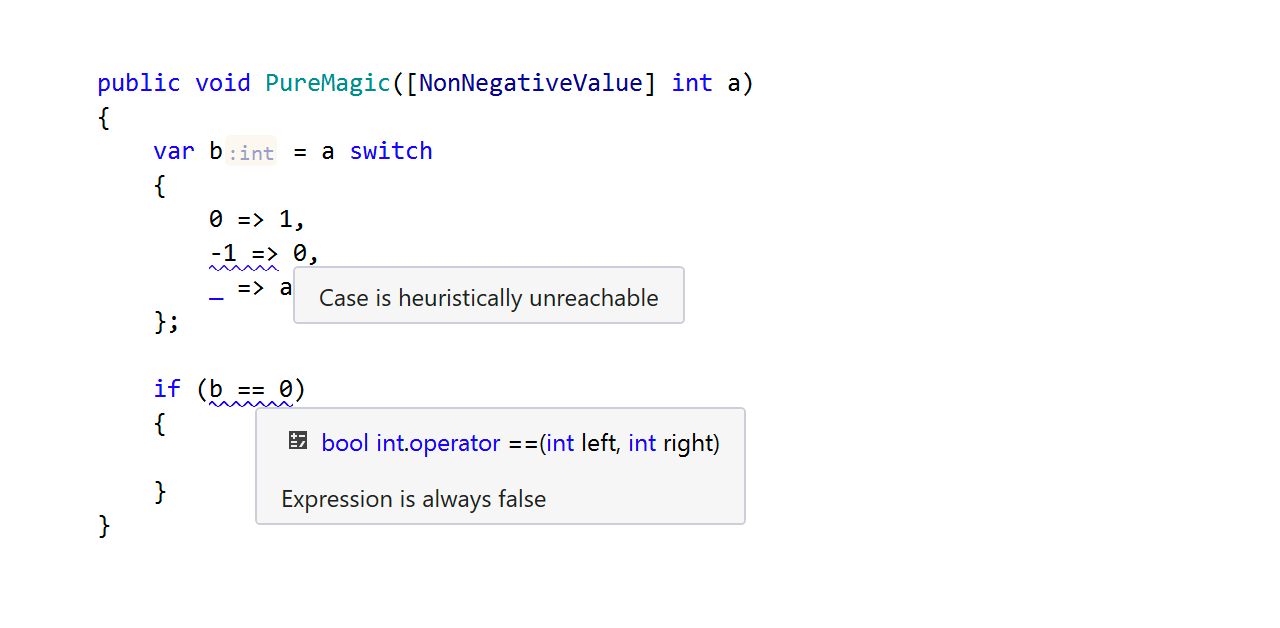
For example, analyzing the piece of code below, we know nothing about the value of parameter x, but we can be certain y is nonnegative since it equals the absolute value of x:

The information on how every integer value can vary is represented as a set of ranges of possible values (which, of course, can be just one range or even just one value).

In the previous example, ReSharper deduced that x lies in the range [int.MinValue, int.MaxValue] and y lies in the range [0, int.MaxValue]. The condition y < 0 is true for all y in the range [int.MinValue, -1], but this range doesn’t overlap with the range of possible values for y, which we deduced earlier. Hence the condition is always false.

Sometimes the analysis can prove that one of the operands in a binary expression is exactly 0 or 1, which opens up new possibilities for reporting warnings. For example, adding a variable with a 0 value is a suspicious operation and can indicate potential errors in the algorithm. This doesn’t apply to addition of literals or constants that equal 0 – if you write x + 0, we assume you know what you are doing.

Looking at the next piece of code, the problem might be that scale has the wrong value, which later results in the meaningless addition of 0:

Our integer analysis knows a few things about System.Math methods and shows specific warnings if it detects suspicious usage of these methods:

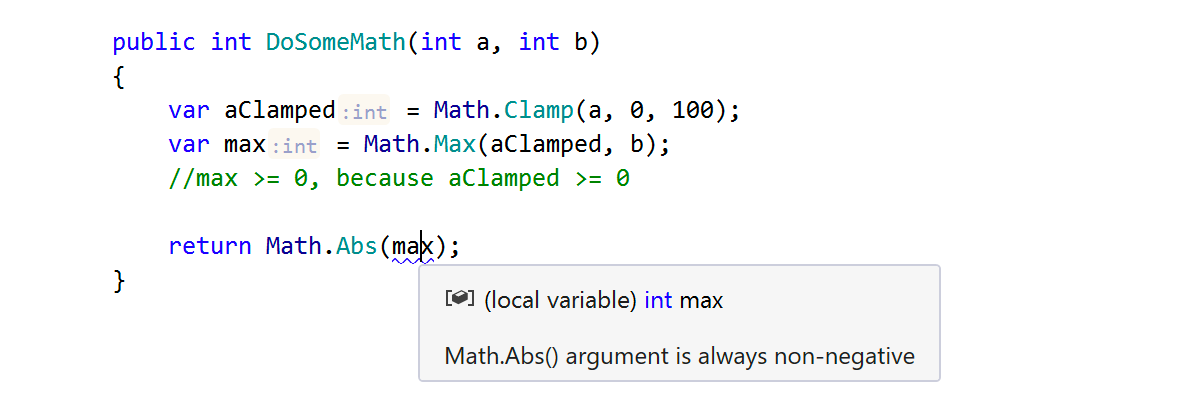
By the way, Math.Clamp is an awesome method that is available in .NET Core and will be available in .NET 5.0. It clamps its first argument value to the inclusive range of min (second argument) and max (third argument). This method has an undocumented exception – it throws a System.ArgumentException when min is greater than max. Our analysis is aware of the checks made by this argument, and it statically checks Clamp invocations for correctness:

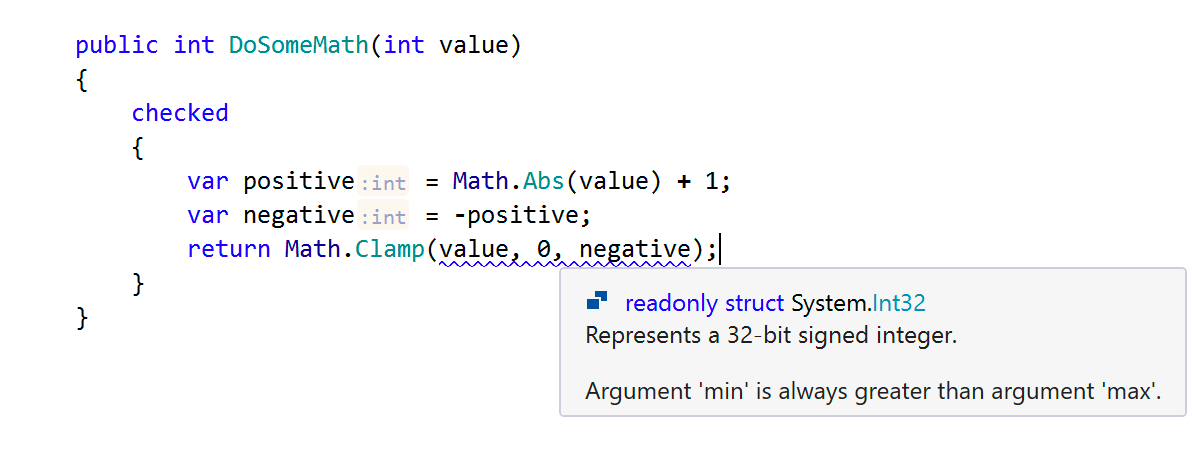
OK, now let’s look at a more interesting example. It is very unlikely that a value equal to the smallest allowed integer (–2,147,483,648) will appear in your program. That you will divide that value by –1 is even less likely. Still, ReSharper will go out on a limb here and warn you about the imminent overflow, because the smallest integer, when negated, doesn’t fall within the range of the int type.

The fun part here is that this operation overflows even in the unchecked context. It happens because on x86 processors, an overflow in a division operation results in a hardware exception (the same exception that you get when dividing by zero). This can seem a bit counterintuitive, because when adding, subtracting, or multiplying, an overflow does not lead to such an exception. If you replace division by multiplication in this example, you’ll notice how it silently overflows – and the ReSharper warning disappears.

In the last example, we also used the [NonNegativeValue] attribute which we will cover in the following section.

New attributes to use with integer type entities

To improve the precision of our dataflow analysis, we’ve added two new JetBrains.Annotations attributes to use with type members, return values, and int parameters: [NonNegativeValue] and [ValueRange(from, to)], to specify how values of particular int members may vary during runtime.

One of the possible applications for these attributes is in methods that can work correctly only with a subset of possible input values. With annotation attributes used for any int parameters of a method, you can get better static checking of arguments at method calls, as well as better code analysis of the method body. This means you will now be able to check the correctness of input values without even running the code :)

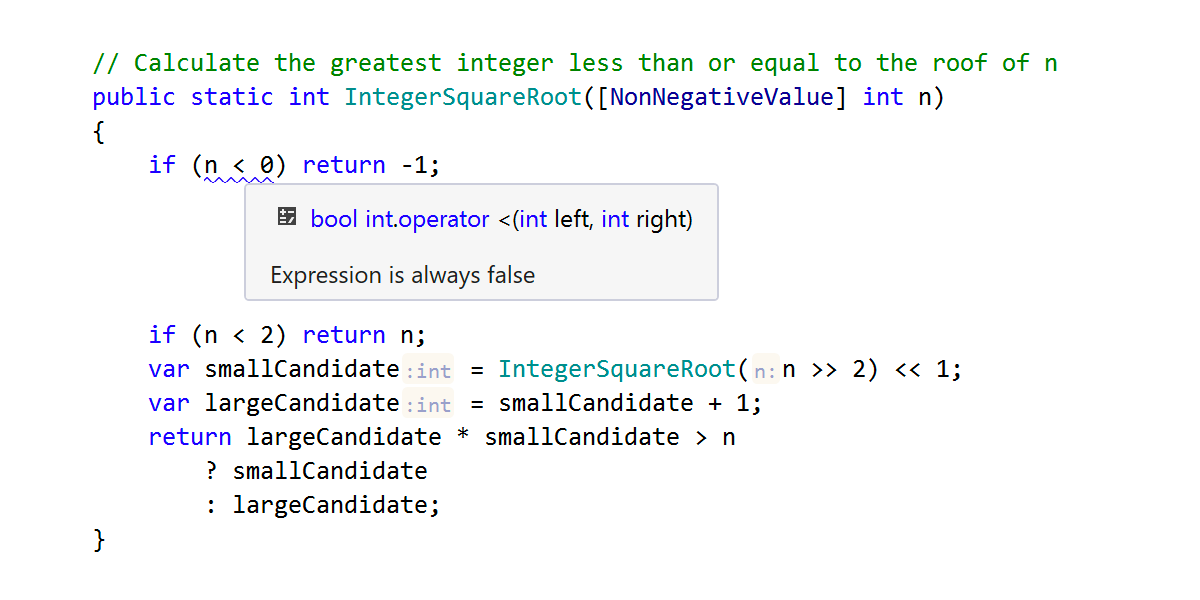
In the following method, the [NonNegativeValue] attribute ensures that the first check of the input parameter becomes redundant, and ReSharper highlights the relational expression accordingly:

What’s more, new attributes can help you avoid checking the return value of the method. All you have to do is annotate the method:

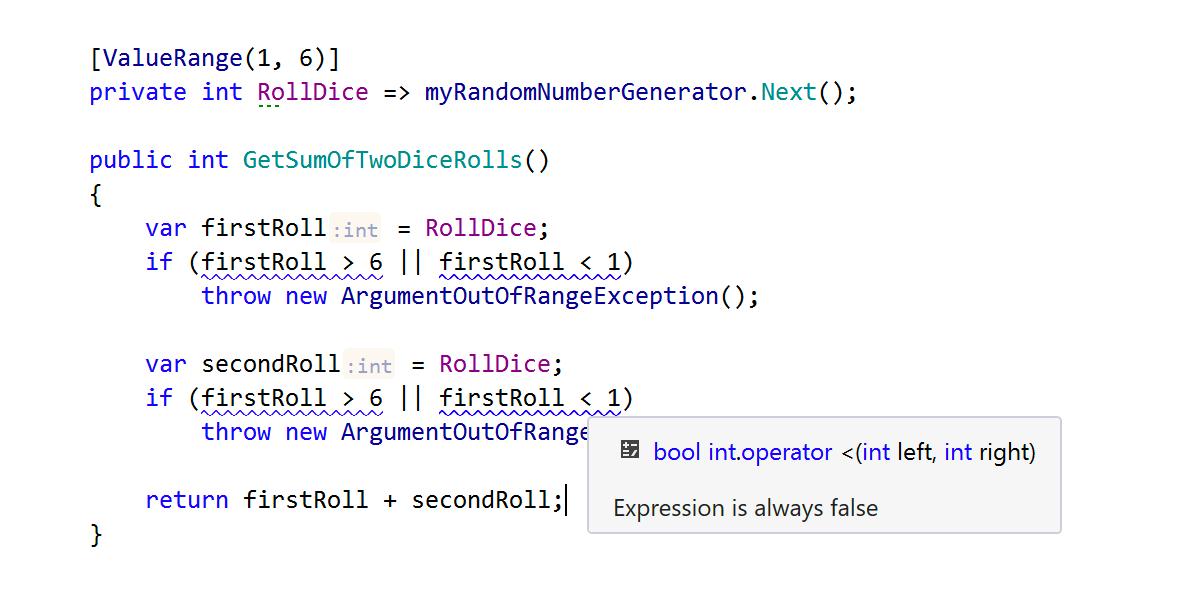
Of course, these attributes can also be used on properties, fields, and indexers.

Looking forward

Integral values analysis was introduced in ReSharper 2020.1 and Rider 2020.1, and our users are already getting some nice warnings thanks to it:

Wow, this is a nice catch. It certainly exceeded my expectations from @JetBrainsRider. pic.twitter.com/VxrWHWtjeX

— ♦️ ěŕëĺíüęŕ˙ ěţěëŕ ♦️ (@vreshetnikov) June 24, 2020

This is just the beginning of our integral values analysis journey. We will continue working on the analysis for the next releases, and this is what we plan to include next:

• Support for other integral types: byte, sbyte, short, ushort, uint, long, and ulong
• Validation of the use of code annotation attributes
• Tracking of array and string lengths

Stay tuned!

Subscribe to a monthly digest curated from the .NET Tools blog:

Subscribe form

By submitting this form, I agree to the JetBrains Privacy Policy Notification icon

By submitting this form, I agree that JetBrains s.r.o. ("JetBrains") may use my name, email address, and location data to send me newsletters, including commercial communications, and to process my personal data for this purpose. I agree that JetBrains may process said data using third-party services for this purpose in accordance with the JetBrains Privacy Policy. I understand that I can revoke this consent at any time in my profile. In addition, an unsubscribe link is included in each email.

Submit

Thanks, we've got you!